|
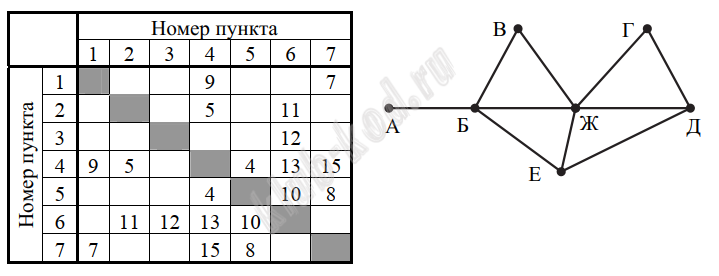
Задание 1. Анализ информационных моделей На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова протяжённость дороги из пункта Г в пункт Ж. В ответе запишите целое число – так, как оно указано в таблице. |
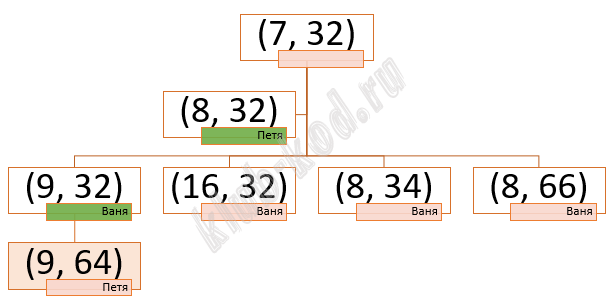
Решение и ответ Анализируя таблицу, мы видим, что только между населенными пунктами 3 и 6, есть одна дорога 36, протяженностью 12 км, причем из пункта 6, кроме данной дороги, выходят еще три, это дороги 62,64 и 65. Рассуждая таким образом, получим граф:
Таким образом, протяженность дороги ГЖ (14) равна 9 км. Ответ: 9
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 2. Построение таблиц истинности логических выражений Миша заполнял таблицу истинности функции (x v y) & ¬(y≡z) & ¬w, но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
|
Решение и ответ  Ответ: ZYXW Ответ: ZYXW
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 3. Базы данных. Файловая система Ниже представлены два фрагмента таблиц из базы данных о жителях микрорайона. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. Определите на основании приведённых данных ID женщины, ставшей матерью в наиболее молодом возрасте. При вычислении ответа учитывайте только информацию из приведённых фрагментов таблиц. 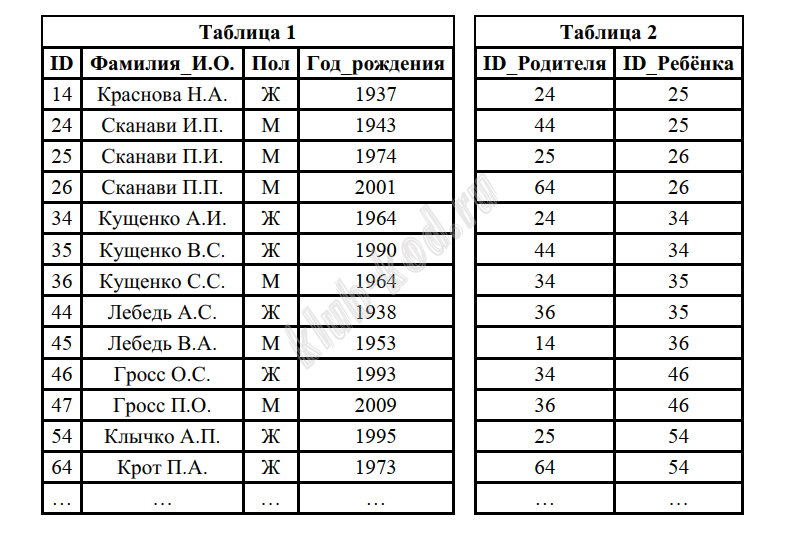 |
Решение и ответ В таблице 2 удобно добавить колонку и посчитать возраст мамы, возраст пап считать не будем (ID родителя мужского пола).
Таким образом, по таблице мы видим, что самой молодой маме было 22 года, это ID родителя 64 Ответ: 64
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 4. Кодирование и декодирование информации Для кодирования некоторой последовательности, состоящей из букв Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся букв – П и Р – кодовые слова неизвестны. Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с наименьшим числовым значением. |
Решение и ответ Поскольку никакое кодовое слово не является началом другого кодового слова, код 10 использовать нельзя, значит получим два слова 100 и 101, из которых наименьшее 100 и будет ответом на вопрос задачи.
Ответ: 100 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 5. Анализ и построение алгоритмов для исполнителей На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1. Строится двоичная запись числа N. 2. К этой записи дописываются справа ещё два разряда по следующему правилу: а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления. |
Решение и ответ Минимальное R, большее 77, это 78.
Мы видим, что подходят по алгоритму числа 78 и 80, из которых 78 наименьшее. Чтобы найти искомое число N, отбросим два дополнительных разряда от найденного 1001110. Правило: Если от двоичного числа отбросить младший разряд, то оно разделится на 2 целочисленным образом (т.е. делим на 2, если есть остаток, убираем его). Уберём второй дополнительный разряд у числа 1001110, получается 78 / 2 = 39 (100111). Уберём ещё и первый дополнительный разряд , получается 39 / 2 = 19 (10011), следовательно двоичное представление искомого числа N равно 10011, а десятичное 19. Ответ: 19 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 6. Анализ программ Определите, при каком наибольшем введённом значении переменной s программа выведет число 64.s = int(input()) |
Решение и ответ Переменная n менялась в цикле от 1 до 64, на каждом шаге, увеличивалась в 2 раза. Построим трассировочную таблицу в обратном порядке.
Наибольшее значение s на первом шаге равно 259. Ответ: 259 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 7. Кодирование и декодирование информации. Передача информации Для хранения произвольного растрового изображения размером 128×320 пикселей отведено 20 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении? |
Решение и ответ N = 2 i, I = K · i , i = I/K I = 20 · 213 бит К = 27 · 25 · 10 = 5 · 213 i = (20 · 213)/ (5 · 213) = 4 бита N = 24 = 16 символов Ответ: 16 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 8. Перебор слов и системы счисления Игорь составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Игорь использует трёхбуквенные слова, в которых могут быть только буквы Ш, К, О, Л, А, причём буква К появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Игорь? |
Решение и ответ ⌈K * * * {Ш, О, Л, А} Получим, 1 · 4 · 4 + 4 · 1 · 4 + 4 · 4 · 1 = 16 + 16 + 16 = 48 Ответ: 48 |
||||||||||||||||||||||||||||||||||||||||||||||||
Задание 9. Работа с таблицами Откройте файл электронной таблицы, содержащей вещественные числа — результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Найдите разность между максимальным значением температуры и её средним арифметическим значением. В ответе запишите только целую часть получившегося числа.Файл с данными
|
Решение и ответ При помощи формул найдем нужные значения: =МАКС(B2:Y92) И их разность, которую округляем до целого Ответ: 14 |
||||||||||||||||||||||||||||||||||||||||||||||||
Задание 10. Поиск символов в текстовом редакторе С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «долг» или «Долг» в тексте романа в стихах А. С. Пушкина «Евгений Онегин». Другие формы слова «долг», такие как «долги», «долгами» и т. д., учитывать не следует. В ответе укажите только число. |
Решение и ответ
В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Оно встречается один раз во фразе "Цензуре долг свой заплачу".
Ответ: 1 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 11. Вычисление количества информации При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 8-символьного набора: А, В, C, D, Е, F, G, H. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 24 байт на одного пользователя. Определите объём памяти (в байтах), необходимый для хранения сведений о 20 пользователях. В ответе запишите только целое число — количество байт. |
Решение и ответ N : { А, В, C, D, Е, F, G, H} – всего 8 различных символов в наборе N = 2 i, 8=23, значит для кодирования одного символа нужно 3 бита I = K · i I = 15 · 3 = 45 бит ≈ 6 байт – отводится на пароль I = 6 + 24 = 30 байт – на одного пользователя (с доп. информацией) I20 = 20 · 30 = 600 байт – всего Ответ: 600 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 12. Выполнение алгоритмов для исполнителей Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется. Цикл выполняется, пока условие истинно. В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно). В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно). Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 70 идущих подряд цифр 8? В ответе запишите полученную строку. НАЧАЛО |
Решение и ответ
s = 70 * '8' print(s) while "2222" in s or "8888" in s: if "2222" in s: s = s.replace( "2222", "88", 1 ) print(s) else: s = s.replace( "8888", "22", 1 ) print(s) 35 раз каждые четыре символа будут заменены на два. Останется 22
Ответ: 22 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
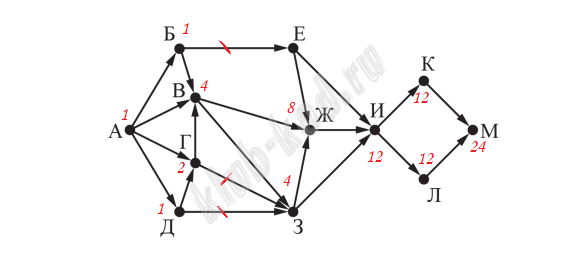
Задание 13. Поиск путей в графе На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.Сколько существует различных путей из города А в город М, проходящих через город В?
|
Решение и ответ
Ответ: 24 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 14. Кодирование чисел. Системы счисления Значение выражения 497 + 721 − 7? записали в системе счисления с основанием 7. Сколько цифр «6» содержится в этой записи? |
Решение и ответ 497 + 721 − 7 = 714 + 721 − 7=100000000000000 + 1000000000000000000000 - 1= В семеричной системе счисления 721 это число, состоящее из 1 и 21 нуля. Ответ: 13 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 15. Преобразование логических выражений Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула |
Решение и ответ
Ответ: 18 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 16. Рекурсивные алгоритмы Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями: F(n) = 1 при n = 1; F(n) = n + F(n − 1), если n — чётно; F(n) = 2 × F(n − 2), если n> 1 и при этом n — нечётно. Чему равно значение функции F(26)?
|
Решение и ответ F(1) = 1
Мы видим, что значения функции от нечетных n представляют из себя степени двойки. F(26) = 26 + F(25) = 26 + 212 = 26 + 4096 = 4122 Ответ: 4122 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 17. Проверка на делимость Рассматривается множество целых чисел, принадлежащих числовому отрезку [1016; 7937], которые делятся на 3 и не делятся на 7, 17, 19, 27. Найдите количество таких чисел и максимальное из них. В ответе запишите два целых числа без пробелов и других дополнительных символов: сначала количество, затем максимальное число. Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц. |
Решение и ответ k=0 m=0 for i in range(1016, 7938): if i % 3 ==0 and i % 7 !=0 and i % 17 !=0 and i % 19 !=0 and i % 27 !=0: k+=1 m=i print (k,m) Ответ: 1568 7935 |
||||||||||||||||||||||||||||||||||||||||||||||||
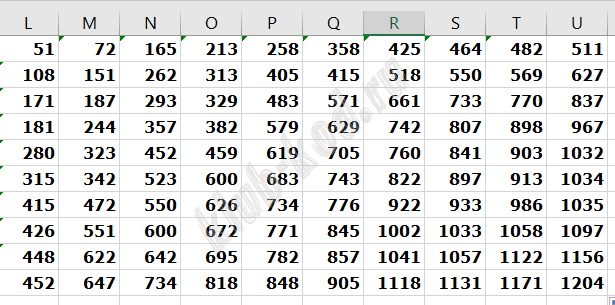
Задание 18. Робот-сборщик монет Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел 41 и 22. |
Решение и ответ 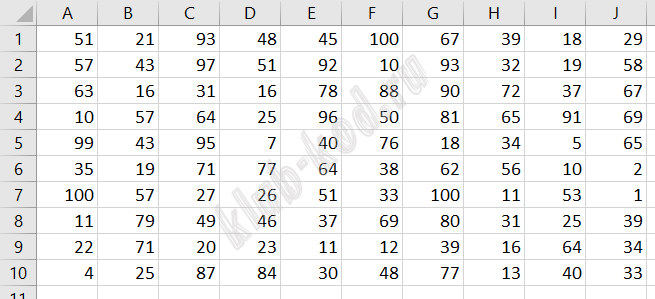
Найдём максимальную денежную сумму. Для этого найдём максимальную денежную сумму для каждой ячейки таблицы. В ячейку L1 запишем формулу =СУММ($A$1:A1). Скопируем эту формулу во все ячейки в диапазоне M1:U1 и в диапазоне L2:L10. Для остальных ячеек будем сравнивать значение ячейки слева и значение ячейки сверху и присваивать текущей ячейке значение суммы той ячейки, в которой значение больше, и текущей ячейки. В M2 запишем формулу =ЕСЛИ(L2>M1;L2+B2;M1+B2) и скопируем эту формулу во все ячейки диапазона M2:U10. Таким образом, в ячейке U10 получим значение максимальной денежной суммы — 1204.
Аналогичным образом найдём значение минимальной денежной суммы. Ячейки диапазонов L1:L10 и M1:U1 заполняются также, как при поиске максимальной денежной суммы. В M2 запишем формулу =ЕСЛИ(L2 < M1;L2+B2;M1+B2) и скопируем эту формулу во все ячейки диапазона M2:U10. Таким образом, в ячейке U10 получим значение минимальной денежной суммы — 502.
Ответ: 1204 502 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 19. Выигрышная стратегия. Задание 1 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем обозначать (10, 5). Тогда за один ход можно получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней. В начальный момент в первой куче было семь камней, во второй куче — S камней; 1 ≤ S ≤ 69. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
|
Решение и ответ Ваня выиграл первым ходом после неудачного хода Пети. Победителем считается игрок, сделавший последний ход, при которой в кучах будет 77 или больше камней. Нужно найти минимальное S, при котором возможна победа Вани. Чтобы S было минимальным, Петя и Ваня удваивали S, значит, (77-7) /4 » 18 . Округляем до целого. Ответ: 18 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 20. Выигрышная стратегия. Задание 2 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем обозначать (10, 5). Тогда за один ход можно получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней. В начальный момент в первой куче было семь камней, во второй куче — S камней; 1 ≤ S ≤ 69. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: — Петя не может выиграть за один ход; — Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания без разделительных знаков. |
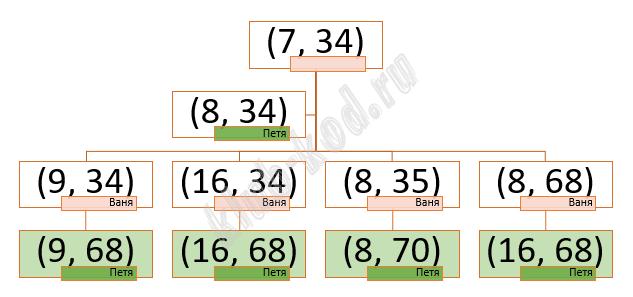
Решение и ответ Значения S 35 и 36 не подходят, поскольку в этом случае Петя может выиграть своим первым ходом. Рассмотрим значение S = 34.
Рассматривая аналогично числа 33 и 32, из дерева мы видим, что комбинации (9, 33) и (9, 32) приведут к победе Вани.
Рассмотрим число 31. Если Петя выбирает комбинацию первого хода (14, 31), то видим на дереве, что она приводит к выигрышу Пети вторым ходом.
Ответ: 3134 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 21. Выигрышная стратегия. Задание 3 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем обозначать (10, 5). Тогда за один ход можно получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней. В начальный момент в первой куче было семь камней, во второй куче — S камней; 1 ≤ S ≤ 69. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника. Найдите минимальное значение S, при котором одновременно выполняются два условия: — у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; — у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. |
Решение и ответ Рассмотрим S=30. Из дерева видим, что данное число камней во второй куче приводит к выигрышу Вани первым или вторым ходом при любой игре Пети. Ответ: 30 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 22. Анализ программы с циклами и условными операторами Дан алгоритм. (код на языке Python). Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 4, а потом 5. x = int(input()) Q = 9 L = 0 while x >= Q: L = L + 1 x = x - Q M = x if M < L: M = L L = x print(L) print(M)
|
Решение и ответ Данный алгоритм ищет два числа: целую часть от деления x на 9 и остаток от деления x на 9. Если остаток от деления числа x на 9 меньше, чем целая часть, то алгоритм меняет местами значения L и M. В результате работы алгоритма на экран будут выведены два числа: 4 и 5. Значит, чтобы найти наибольшее число x, число 5 должно являться целой частью от деления x на 9, а число 4 — остатком от деления x на 9. То есть, x = 9 · 5 + 4 = 49. Ответ: 49 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 23. Анализ программы с циклами и условными операторами Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера: 1. Прибавить 1 Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя — это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 20 и при этом траектория вычислений содержит число 10? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17. |
Решение и ответ 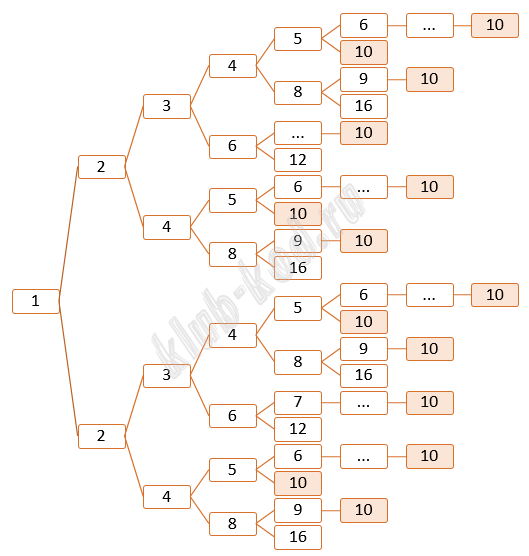
Данное дерево вариантов показывает программы получения 10 из 1. Всего мы видим 14 различных вариантов. Чтобы получить из числа 10 число 20, есть два варианта, последовательно прибавлять 1 или умножить на 2. То есть 14 * 2 = 28 Ответ: 28 |
||||||||||||||||||||||||||||||||||||||||||||||||
Задание 24. Анализ программы с циклами и условными операторами Текстовый файл состоит не более чем из 106 символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых каждые два соседних различны. Для выполнения этого задания следует написать программу. |
Решение и ответ with open("24.txt", "r") as f: for i in range(2,len(s)): print(m) Ответ: 35 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание 25. Анализ программы с циклами и условными операторами Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [174457; 174505], числа, имеющие ровно два различных натуральных делителя, не считая единицы и самого числа. Для каждого найденного числа запишите эти два делителя в два соседних столбца на экране с новой строки в порядке возрастания произведения этих двух делителей. Делители в строке также должны следовать в порядке возрастания. Например, в диапазоне [5; 9] ровно два различных натуральных делителя имеют числа 6 и 8, поэтому для этого диапазона вывод на экране должна содержать следующие значения: 2 3 |
Решение и ответ for i in range(174457, 174506): |
||||||||||||||||||||||||||||||||||||||||||||||||
Задание 26. Анализ программы с циклами и условными операторами Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя. По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей. В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 10 000) и N — количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке. Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей. Пример входного файла: 100 4 При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера: 2 50 |
Решение и ответ f = open("26.txt", "r") st=f.readline().split() S=int(st[0]) # размер свободного места на диске N=int(st[1]) # количество пользователей I=0 # объем файлов пользователей del(st) P=[int(i) for i in f] # массив файлов пользователей P.sort() #сортируем по возрастанию k=0 #количество файлов, которые смогут поместиться на диске for i in P: m=0 # максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей for i in range(len(P)): print(k,m) Ответ: 568 50 |
||||||||||||||||||||||||||||||||||||||||||||||||
Задание 27. Анализ программы с циклами и условными операторами Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 3 и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число — максимально возможную сумму, соответствующую условиям задачи. Входные данные Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество пар N (1 ≤ N ≤ 100000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 10 000. Пример организации исходных данных во входном файле: 6 Для указанных входных данных значением искомой суммы должно быть число 32.В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B. Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго. |
Решение и ответ with open("27-A.txt", "r") as f: for i in range(k): if s%3!=0: Ответ: 127127 399762080 |
||||||||||||||||||||||||||||||||||||||||||||||||
В решение заданий демо-версии 2021 используется язык программирования Python.
- Разбор демо-версий
- Просмотров: 7309