15. Логические выражения

: Сборник ЕГЭ-2023; 05 февраля 2023; Просмотров: 26172

Задание 15. Преобразование логических выражений

Рейтинг: 4 / 5

ВАРИАНТ 1

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наименьшего натурального числа А формула

(ДЕЛ(x, 13) → ¬(ДЕЛ(x, 21) v (x + A >= 500))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x?

Решение и ответ

def d(n, m):
if n % m == 0: #проверка на делимость
return 1

for A in range (1,1000):
OK = True
for x in range (1,1000):
OK*=( not(d(x,13)) or not(d(x,21)) or (x + A) >= 500 )
if OK: # истинность для любого х
print (A)
break

Ответ: 227

ВАРИАНТ 2

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наименьшего натурального числа А формула

(ДЕЛ(x, 20) → ¬(ДЕЛ(x, 11) v (x + A >= 300))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x?

Решение и ответ

def d(n, m):
if n % m == 0: #проверка на делимость
return 1

for A in range (1,1000):
OK = True
for x in range (1,1000):
OK*=( not(d(x,20)) or not(d(x,11)) or (x + A) >= 300 )
if OK: # истинность для любого х
print (A)
break

Ответ: 80

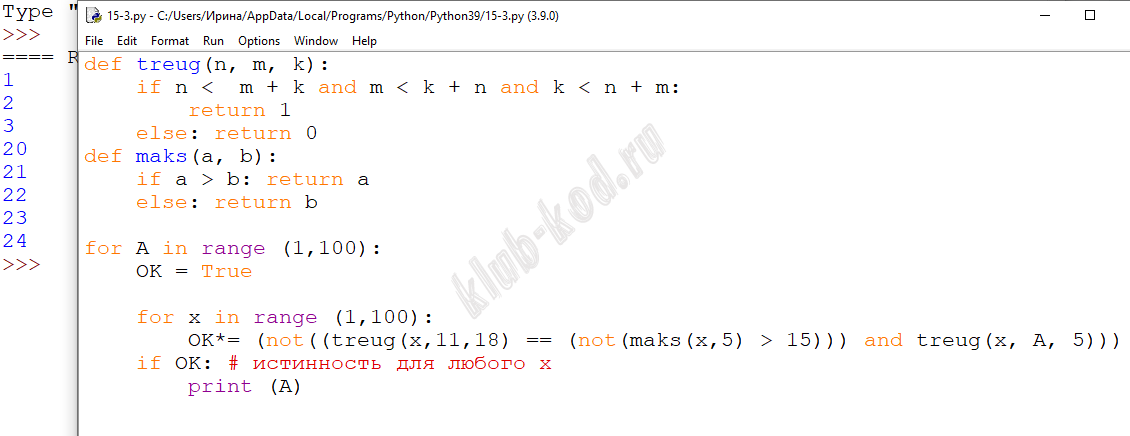
ВАРИАНТ 3

Обозначим через ТРЕУГ(n, m, k) утверждение «существует невырожденный треугольник с длинами сторон n, m и k».

Для какого наибольшего натурального числа А формула

¬((ТРЕУГ(х, 11, 18) ≡ (¬(МАКС(x, 5) >15))) & ТРЕУГ(x, A, 5))

тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной x?

Примечание: МАКС(a, b) = a, если a > b и МАКС (a, b) = b, если a <= b

Решение и ответ

Треугольник называется невырожденным, если его площадь больше 0, то есть вершины не лежат на одной прямой.

Ответ: 24

ВАРИАНТ 4

Обозначим через ТРЕУГ(n, m, k) утверждение «существует невырожденный треугольник с длинами сторон n, m и k».

Для какого наибольшего натурального числа А формула

¬((ТРЕУГ(х, 12, 20) ≡ (¬(МАКС(x, 5) >28))) & ТРЕУГ(x, A, 3))

тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной x?

Примечание: МАКС(a, b) = a, если a > b и МАКС (a, b) = b, если a <= b

Решение и ответ

def treug(n, m, k):
if n < m + k and m < k + n and k < n + m:
return 1
else: return 0

for A in range (1,100):
OK = True

for x in range (1,100):
OK*= (not((treug(x, 12, 20) == (not(max(x, 5) > 28))) and treug(x, A, 3)))
if OK: # истинность для любого х
print (A)

Ответ: 6

ВАРИАНТ 5

На числовой прямой даны два отрезка: B = [10, 15] и C = [20, 27]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
¬(((x ∈ B) v (x ∈ C)) → (x ∈ A))ложно(то есть принимает значение 0) при любом значении переменной х.

Решение и ответ

B = [i for i in range(10,16)]
C = [i for i in range(20,28)]
A = []

for x in range(100):
if not( ((x in B) or (x in C)) <= (x in A) ):
A.append(x)# добавляем в массив А все х, для которых выражение ложно
print(max(A) - min(A)) #находим разницу между макс и мин значением элементов массива

Ответ: 17

ВАРИАНТ 6

На числовой прямой даны два отрезка: B = [30, 41] и C = [50, 56]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение

¬(((x ∈ B) v (x ∈ C)) → (x ∈ A))

ложно(то есть принимает значение 0) при любом значении переменной х.

Решение и ответ

B = [i for i in range(30,42)]
C = [i for i in range(50,57)]
A = []

for x in range(100):
if not (((x in B) or (x in C)) <= (x in A)):
A.append(x)
print(max(A) - min(A))

Ответ: 26

ВАРИАНТ 7

На числовой прямой даны два отрезка: B = [14, 20] и C = [15, 27]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение

¬(x ∈ A) → ((x ∈ B)) ≡ (x ∈ C))

истинно (то есть принимает значение 1) при любом значении переменной х.

Решение и ответ

B = [i for i in range(14,21)]
C = [i for i in range(15,28)]
A = []

for x in range(1,100):
if not(not(x in A)) <= ((x in B) == (x in C)) : # внимание, скобки!
A.append(x)
print(max(A)- min(A))

Ответ: 13

ВАРИАНТ 8

На числовой прямой даны два отрезка: B = [4, 18] и C = [12, 40]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение

¬(x ∈ A) → ((x ∈ B)) ≡ (x ∈ C))

истинно (то есть принимает значение 1) при любом значении переменной х.

Решение и ответ

B = [i for i in range(4,19)]
C = [i for i in range(12,41)]
A = []

for x in range(1,100):
if not(not(x in A)) <= ((x in B) == (x in C)) : # внимание, скобки!
A.append(x)
print(max(A)- min(A))

Ответ: 36

ВАРИАНТ 9

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наибольшего натурального числа А формула

¬ДЕЛ(x, А) → (ДЕЛ(x, 18) → ¬ДЕЛ(x, 81))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?

Решение и ответ

Ответ: 162

ВАРИАНТ 10

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наибольшего натурального числа А формула

¬ДЕЛ(x, А) → (ДЕЛ(x, 26) → ¬ДЕЛ(x, 169))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?

Решение и ответ

Ответ: 26

ВАРИАНТ 11

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наибольшего натурального числа А формула

¬ДЕЛ(x, А) → (ДЕЛ(x, 24) → ¬ДЕЛ(96, х))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?

Решение и ответ

for A in range (1,100):
OK = True
for x in range (1,100):
OK *= ( (x % A != 0) <= ((x % 24 == 0) <= (96 % x !=0)) ) # внимание, скобки!

if OK: # истинность для любого х
print (A)

Ответ: 24

ВАРИАНТ 12

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наибольшего натурального числа А формула

¬ДЕЛ(x, А) → (ДЕЛ(x, 54) → ¬ДЕЛ(162, х))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?

Решение и ответ

for A in range (1,100):
OK = True
for x in range (1,100):
OK *= ( (x % A != 0) <= ((x % 54 == 0) <= (162 % x !=0)) ) # внимание, скобки!

if OK: # истинность для любого х
print (A)

Ответ: 54

ВАРИАНТ 13

Для какого наибольшего целого неотрицательного числа А выражение

(х >= A) v (y >= A) v (x · y <= 200)

тождественно истинно, т.е. принимает значение 1 при любых целых положительных х и у?

Решение и ответ

for A in range (0,100):
OK = True
for x in range (1,100):
for y in range (1, 100):
OK *= ( (x >= A) or (y >= A) or (x*y <= 200))

if OK: # истинность для любого х
print (A)

Ответ: 15

ВАРИАНТ 14

Для какого наибольшего целого неотрицательного числа А выражение

(х >= A) v (y >= A) v (x · y <= 270)

тождественно истинно, т.е. принимает значение 1 при любых целых положительных х и у?

Решение и ответ

for A in range (0,100):
OK = True
for x in range (1,100):
for y in range (1, 100):
OK *= ( (x >= A) or (y >= A) or (x*y <= 270))

if OK: # истинность для любого х
print (A)

Ответ: 17

ВАРИАНТ 15

Для какого наибольшего целого неотрицательного числа А выражение

(х < A) & (y < A) & (x · y > 601)

тождественно ложно, т.е. принимает значение 0 при любых целых положительных х и у?

Решение и ответ

for A in range (0,100):
OK = True
for x in range (1,100):
for y in range (1, 100):
OK *= not( (x < A) and (y < A) and (x*y > 601))

if OK: # истинность для любого х
print (A)

Ответ: 25

ВАРИАНТ 16

Для какого наибольшего целого неотрицательного числа А выражение

(х < A) & (y < A) & (x · y > 1200)

тождественно ложно, т.е. принимает значение 0 при любых целых положительных х и у?

Решение и ответ

for A in range (0,100):
OK = True
for x in range (1,100):
for y in range (1, 100):
OK *= not( (x < A) and (y < A) and (x*y > 1200))

if OK: # истинность для любого х
print (A)

Ответ: 35

ВАРИАНТ 17

Для какого наименьшего целого числа А формула

(3 * х + у < A) v (x < y) v (16 <= x)

тождественно истинна, т.е. принимает значение 1 при любых целых положительных х и у?

Решение и ответ

for A in range (-100,100):
OK = True
for x in range (1,100):
for y in range (1, 100):
OK *= (((3 * x + y) < A) or (x < y) or (16 <= x))
if OK: # истинность для любого х
print (A)
break

Ответ: 61

ВАРИАНТ 18

Для какого наименьшего целого числа А формула

(2 * х + у < A) v (x < y) v (21 <= x)

тождественно истинна, т.е. принимает значение 1 при любых целых положительных х и у?

Решение и ответ

for A in range (-100,100):
OK = True
for x in range (1,100):
for y in range (1, 100):
OK *= (((2 * x + y) < A) or (x < y) or (21 <= x))
if OK: # истинность для любого х
print (A)
break

Ответ: 61

ВАРИАНТ 19

Для какого наименьшего целого числа А формула

(y + 5 * х <= 34) <= ((y - x > 4) v (y <= A)

тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных и у?

Решение и ответ

for A in range (-100,100):
OK = True
for x in range (0,100):
for y in range (0, 100):
OK *= ((5 * x + y) <= 34) <= ((y - x > 4) or (y <= A))

if OK: # истинность для любого х
print (A)
break

Ответ: 9

ВАРИАНТ 20

Для какого наименьшего целого числа А формула

(y + 2 * х <= 27) <= ((y - x > 3) v (y <= A)