|
ВАРИАНТ 1 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) Далее если исходное число четное, то справа к построенной двоичной записи числа N приписывается 0, если нечетное, то приписывается 1. 3) Далее полученная на втором шаге алгоритма запись обрабатывается по следующему правилу: а) если количество единиц в двоичной записи кратно трем, то в этой записи два левых разряда заменяются на 11; б) если количество единиц в двоичной записи некратно трем, то в этой записи два левых разряда заменяются на 10. Полученная таким образом запись является двоичной записью искомого числа R. Например, для исходного числа 610 = 1102 результатом является число 10002 = 810, а для исходного числа 310 = 112, результатом является число 1112 = 710.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, не меньшее чем 26. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ
Ответ: 9 |
||
|
ВАРИАНТ 2 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) Далее если исходное число четное, то справа к построенной двоичной записи числа N приписывается 0, если нечетное, то приписывается 1. 3) Далее полученная на втором шаге алгоритма запись обрабатывается по следующему правилу: а) если количество единиц в двоичной записи кратно трем, то в этой записи два левых разряда заменяются на 11; б) если количество единиц в двоичной записи некратно трем, то в этой записи два левых разряда заменяются на 10. Полученная таким образом запись является двоичной записью искомого числа R. Например, для исходного числа 610 = 1102 результатом является число 10002 = 810, а для исходного числа 310 = 112, результатом является число 1112 = 710.
Укажите максимальное число N, после обработки которого с помощью этого алгоритма получается число R, не большее чем 37. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ Решение как в первом варианте.
for x in range(1,30): #перебираем х if N.count('1')%3 == 0: # преобразование 3 шага print(x, int(R,2)) # переводим R в десятичную систему счисления Из таблицы значений видим, что наибольшее N = 25 для R = 35 Ответ: 25 |
||
|
ВАРИАНТ 3 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) Далее эта запись обрабатывается по следующему правилу: а) если количество значащих цифр в двоичной записи числа четное, то к этой записи в середину дописывается 1; б) если количество значащих цифр в двоичной записи числа нечетное, то запись не изменяется. Полученная таким образом запись является двоичной записью искомого числа R. Например, для исходного числа 510 = 1012 результатом является число 1012 = 510, а для исходного числа 210 = 102, результатом является число 1102 = 610.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, не меньшее чем 26. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ for x in range(1,30): #перебираем х N=bin(x)[2:] #получаем двоичную запись, убираем первые 2 символа 0b if len(N)%2 == 0: R = N[:len(N)//2] + '1' +N[len(N)//2:] else: R = N print(x, int(R,2)) # переводим R в десятичную систему счисления
Ответ: 12 |
||
|
ВАРИАНТ 4 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) Далее эта запись обрабатывается по следующему правилу: а) если количество значащих цифр в двоичной записи числа четное, то к этой записи в середину дописывается 1; б) если количество значащих цифр в двоичной записи числа нечетное, то запись не изменяется. Полученная таким образом запись является двоичной записью искомого числа R. Например, для исходного числа 510 = 1012 результатом является число 1012 = 510, а для исходного числа 210 = 102, результатом является число 1102 = 610.
Укажите максимальное число N, после обработки которого с помощью этого алгоритма получается число R, не большее чем 26. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ for x in range(1,30): #перебираем х N=bin(x)[2:] #получаем двоичную запись, убираем первые 2 символа 0b if len(N)%2 == 0: R = N[:len(N)//2] + '1' +N[len(N)//2:] else: R = N print(x, int(R,2)) # переводим R в десятичную систему счисления
Ответ: 26 |
||
|
ВАРИАНТ 5 Автомат получает на вход трехзначное число. По этому число строится новое число по следующим правилам: 1. Вычисляются суммы квадратов первой и второй, а также второй и третьей цифр исходного числа. 2. Полученные два числа записываются друг за другом в порядке невозрастания (без разделителей).
Пример. Исходное число: 621. Суммы квадратов цифр: 62 + 22 = 40; 22 + 12 = 5. Результат: 405. Укажите наибольшее число, в результате обработки которого автомат выдаст число 9752. |
Решение и ответ for x in range(100,1000): a= x//100 b = (x//10)%10 c = x % 10 if (a ** 2 + b**2 == 97 and b**2 + c**2 == 52) or (a ** 2 + b**2 == 52 and b**2 + c**2 == 97): print(a*100 +b*10+c) Ответ: 946 |
||
|
ВАРИАНТ 6 Автомат получает на вход трехзначное число. По этому число строится новое число по следующим правилам: 1. Вычисляются суммы квадратов первой и второй, а также второй и третьей цифр исходного числа. 2. Полученные два числа записываются друг за другом в порядке невозрастания (без разделителей).
Пример. Исходное число: 621. Суммы квадратов цифр: 62 + 22 = 40; 22 + 12 = 5. Результат: 405. Укажите наибольшее число, в результате обработки которого автомат выдаст число 7434. |
Решение и ответ for x in range(100,1000):
a= x//100 if (a ** 2 + b**2 == 74 and b**2 + c**2 == 34) or (a ** 2 + b**2 == 34 and b**2 + c**2 == 74): print(a*100 +b*10+c) Ответ: 753 |
||
|
ВАРИАНТ 7 Автомат получает на вход трехзначное число. По этому число строится новое число по следующим правилам: 1. Перемножаются все цифры исходного числа. 2. Суммируются все цифры исходного числа. 3. Полученные два числа записываются друг за другом в порядке невозрастания (без разделителей).
Пример. Исходное число: 621. Произведение цифр 6х2х1 = 12. Суммы цифр: 6 + 2 + 1 = 9 Результат: 129. Укажите наибольшее число, в результате обработки которого автомат выдаст число 33621. |
Решение и ответ for x in range(100,1000): if p == 336 and s == 21: Ответ: 876 |
||
|
ВАРИАНТ 8 Автомат получает на вход трехзначное число. По этому число строится новое число по следующим правилам: 1. Перемножаются все цифры исходного числа. 2. Суммируются все цифры исходного числа. 3. Полученные два числа записываются друг за другом в порядке невозрастания (без разделителей).
Пример. Исходное число: 621. Произведение цифр 6х2х1 = 12. Суммы цифр: 6 + 2 + 1 = 9 Результат: 129. Укажите наибольшее число, в результате обработки которого автомат выдаст число 24019. |
Решение и ответ for x in range(100,1000): if p == 240 and s == 19: Ответ: 865 |
||
|
ВАРИАНТ 9 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Из числа N вычитается остаток от деления N на 4. 2) Строится двоичная запись полученного результата. 3) К этой записи дописываются справа еще два разряда по следующему правилу: а) складываются все цифры построенной двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; б) над этой записью производятся те же действия - справа дописывается остаток от деления суммы ее цифр на 2. Полученная таким образом запись является двоичной записью искомого числа R.
Укажите минимальное число R, большее 56, которое может являться результатом работы данного алгоритма. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ for x in range(5,20): #перебираем х if N.count('1')%2 == 0: print(x, int(R,2)) # переводим R в десятичную систему счисления Ответ: 66 |
||
|
ВАРИАНТ 10 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Из числа N вычитается остаток от деления N на 4. 2) Строится двоичная запись полученного результата. 3) К этой записи дописываются справа еще два разряда по следующему правилу: а) складываются все цифры построенной двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; б) над этой записью производятся те же действия - справа дописывается остаток от деления суммы ее цифр на 2. Полученная таким образом запись является двоичной записью искомого числа R.
Укажите минимальное число R, большее 100, которое может являться результатом работы данного алгоритма. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ Решение как в варианте 9.
for x in range(20,35): #перебираем х N = x - x % 4 if N.count('1')%2 == 0: print(x, int(R,2)) # переводим R в десятичную систему счисления Из таблицы полученных значений мы видим, что минимальное больше 100, R=114. Ответ: 114 |
||
|
ВАРИАНТ 11 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Из числа N вычитается остаток от деления N на 4. 2) Строится двоичная запись полученного результата. 3) К этой записи дописываются справа еще два разряда по следующему правилу: а) складываются все цифры построенной двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; б) над этой записью производятся те же действия - справа дописывается остаток от деления суммы ее цифр на 2. Полученная таким образом запись является двоичной записью искомого числа R. Укажите наибольшее число N, для которого результат работы данного алгоритма меньше числа 64. В ответе запишите это число в десятичной системе счисления.
|
Решение и ответ Решение как в варианте 9.
for x in range(10,35): #перебираем х if N.count('1')%2 == 0: print(x, int(R,2)) # переводим R в десятичную систему счисления Из таблицы полученных значений мы видим, что наибольшее N=15, соответствует R=48 Ответ: 15 |
||
|
ВАРИАНТ 12 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Из числа N вычитается остаток от деления N на 4. 2) Строится двоичная запись полученного результата. 3) К этой записи дописываются справа еще два разряда по следующему правилу: а) складываются все цифры построенной двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; б) над этой записью производятся те же действия - справа дописывается остаток от деления суммы ее цифр на 2. Полученная таким образом запись является двоичной записью искомого числа R.
Укажите наибольшее число N, для которого результат работы данного алгоритма меньше числа 47. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ Решение как в варианте 9.
Из таблицы полученных значений мы видим, что наибольшее N=11, соответствует R=34. Ответ: 11 |
||
|
ВАРИАНТ 13 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Из числа N вычитается остаток от деления N на 8, после чего прибавляется остаток от деления N на 2. 2) Строится двоичная запись полученного результата. 3) К этой записи дописываются справа еще два разряда по следующему правилу: а) складываются все цифры построенной двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; б) над этой записью производятся те же действия - справа дописывается остаток от деления суммы ее цифр на 2. Полученная таким образом запись является двоичной записью искомого числа R.
Укажите минимальное число R, большее 90, которое может являться результатом работы данного алгоритма. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ for x in range(10,35): #перебираем х if N.count('1')%2 == 0: if N.count('1')%2 == 0: print(x, int(R,2)) # переводим R в десятичную систему счисления Из таблицы полученных значений мы видим, что наименьшее, большее 90, R=96. Ответ: 96 |
||
|
ВАРИАНТ 14 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Из числа N вычитается остаток от деления N на 8, после чего прибавляется остаток от деления N на 2. 2) Строится двоичная запись полученного результата. 3) К этой записи дописываются справа еще два разряда по следующему правилу: а) складываются все цифры построенной двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; б) над этой записью производятся те же действия - справа дописывается остаток от деления суммы ее цифр на 2. Полученная таким образом запись является двоичной записью искомого числа R.
Укажите минимальное число R, большее 97, которое может являться результатом работы данного алгоритма. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ Решение как в варианте 13.
Из таблицы полученных значений мы видим, что наименьшее, большее 97, R=130. Ответ: 130 |
||
|
ВАРИАНТ 15 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) Каждый разряд этой записи заменяется двумя разрядами по следующему правилу: если в разряде стоит 0, то вместо него пишется 00; если в разряде стоит 1, то 1 заменяется на 11. Например, двоичная запись 1001 числа 9 будет преобразована в 11000011. Полученная таким образом запись (в ней в два раза больше разрядов, чем в записи исходного числа N) является двоичной записью искомого числа R - результата работы данного алгоритма.
Укажите минимальное число R, большее 32 которое может являться результатом работы данного алгоритма. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ for x in range(1,50): #перебираем х R = int(N,2)# переводим R в десятичную систему счисления print(x, R) Из таблицы полученных значений мы видим, что наименьшее, большее 32, R = 48. Ответ: 48 |
||
|
ВАРИАНТ 16 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) Каждый разряд этой записи заменяется двумя разрядами по следующему правилу: если в разряде стоит 0, то вместо него пишется 00; если в разряде стоит 1, то 1 заменяется на 11. Например, двоичная запись 1001 числа 9 будет преобразована в 11000011. Полученная таким образом запись (в ней в два раза больше разрядов, чем в записи исходного числа N) является двоичной записью искомого числа R - результата работы данного алгоритма.
Укажите минимальное число R, большее 63 которое может являться результатом работы данного алгоритма. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ Решение как в варианте 15.
Из таблицы полученных значений мы видим, что наименьшее, большее 63, R = 192. Ответ: 192 |
||
|
ВАРИАНТ 17 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) Каждый разряд этой записи заменяется двумя разрядами по следующему правилу: если в разряде стоит 0, то вместо него пишется 01; если в разряде стоит 1, то 1 заменяется на 10. Например, двоичная запись 1001 числа 9 будет преобразована в 10010110. Полученная таким образом запись (в ней в два раза больше разрядов, чем в записи исходного числа N) является двоичной записью искомого числа R - результата работы данного алгоритма.
Укажите минимальное число R, большее 63 которое может являться результатом работы данного алгоритма. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ for x in range(5,20): #перебираем х print(N) print(x, R) Из таблицы полученных значений мы видим, что наименьшее, большее 63, R = 149. Ответ: 149 |
||
|
ВАРИАНТ 18 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) Каждый разряд этой записи заменяется двумя разрядами по следующему правилу: если в разряде стоит 0, то вместо него пишется 01; если в разряде стоит 1, то 1 заменяется на 10. Например, двоичная запись 1001 числа 9 будет преобразована в 10010110. Полученная таким образом запись (в ней в два раза больше разрядов, чем в записи исходного числа N) является двоичной записью искомого числа R - результата работы данного алгоритма.
Укажите максимальное нечетное число R, меньшее 256 которое может являться результатом работы данного алгоритма. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ Решение как в варианте 17.
Из таблицы полученных значений мы видим, что максимальное нечетное , меньшее 256, R = 169. Ответ: 169 |
||
|
ВАРИАНТ 19 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) К этой записи дописываются справа еще два разряда по следующему правилу: если N делится нацело на 4, в конец числа (справа) дописывается сначала 0, а затем еще один 0; если N при делении на 4 дает остаток 1, то в конец числа (справа) дописывается сначала 0, потом 1; если N при делении на 4 дает остаток 2, то в конец числа (справа) дописывается сначала 1, потом 0; если N при делении на 4 дает остаток 3, то в конец числа (справа) дописывается сначала 1, затем еще 1. Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110000. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R - результата работы данного алгоритма.
Укажите максимальное число R, которое меньше 100 и может являться результатом работы данного алгоритма. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ for x in range(5,30): #перебираем х R = int(N,2)# переводим R в десятичную систему счисления print(x, R) Из таблицы полученных значений мы видим, что наибольшее R, меньшее 100, равно 96. Ответ: 96 |
||
|
ВАРИАНТ 20 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) К этой записи дописываются справа еще два разряда по следующему правилу: если N делится нацело на 4, в конец числа (справа) дописывается сначала 0, а затем еще один 0; если N при делении на 4 дает остаток 1, то в конец числа (справа) дописывается сначала 0, потом 1; если N при делении на 4 дает остаток 2, то в конец числа (справа) дописывается сначала 1, потом 0; если N при делении на 4 дает остаток 3, то в конец числа (справа) дописывается сначала 1, затем еще 1. Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110000. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R - результата работы данного алгоритма.
Укажите максимальное число R, которое меньше 111 и может являться результатом работы данного алгоритма. В ответе запишите это число в десятичной системе счисления. |
Решение и ответ Из таблицы полученных значений мы видим, что максимальное R, меньшее 111, равно 106. Ответ: 106 |
- Сборник ЕГЭ-2023
- Просмотров: 42971
Задание 05. Анализ и построение алгоритмов для исполнителей
Комментарии






Добавить комментарий
0
#
сон
10.05.2024 16:22
в варианте 14 правильный ответ 102, а не 130
Ответить
| Ответить с цитатой |
Цитировать
|
Сообщить модератору
0
#
Ирина
12.05.2024 20:03
Перепроверила, минимальное R, большее 97 - это 130. Ответ сходится с авторами сборника
Ответить
| Ответить с цитатой |
Цитировать
|
Сообщить модератору
0
#
acquaintance
12.01.2024 10:19
Во втором варианте в преобразовании 2 шага должна проверяться чётность исходного числа, а не преобразованного. Правильный ответ 25, но при выводе работы указанного кода присутствует число R, равное 37, что удовлетворяет условию и этому числу соответствует 26. Вывод: см. первое предложение.
Ответить
| Ответить с цитатой |
Цитировать
|
Сообщить модератору
0
#
админ
13.01.2024 00:17
Здесь не соглашусь. Все четные двоичные числа оканчиваются на 0. Во втором варианте код выдает таблицу, в которой числу 26 соответствует R = 52. Ответ - 25.
Ответить
| Ответить с цитатой |
Цитировать
|
Сообщить модератору
0
#
acquaintance
10.01.2024 17:06
функция str() в формате str(bin()) не обязательна, т.к. значение полученное с помощью bin() в Python по умолчанию строка
Ответить
| Ответить с цитатой |
Цитировать
|
Сообщить модератору
0
#
админ
13.01.2024 00:09
Спасибо за комментарий! Принято и исправлено!
Ответить
| Ответить с цитатой |
Цитировать
|
Сообщить модератору




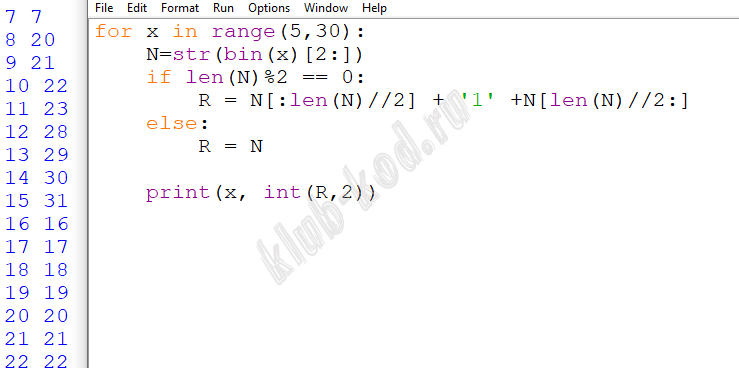 Из таблицы значений видим, что наименьшее N = 12 для R = 28
Из таблицы значений видим, что наименьшее N = 12 для R = 28