Задание 26. Обработка целочисленной информации

: Сборник ЕГЭ-2023; 14 апреля 2023; Просмотров: 6036

Задание 26. Обработка целочисленной информации

Рейтинг: 5 / 5

ВАРИАНТ 1

В тематическом парке для строительства арт-объектов используются однородные прямые круговые цилиндры с одинаковыми высотами; таких цилиндров заготовлено N штук. Руководством парка рабочим поставлена задача создать максимальной высоты пирамиду из поставленных друг на друга цилиндров, такую, чтобы каждый следующий цилиндр имел радиус основания не менее чем на 7 единиц меньше, чем предыдущий, чтобы у посетителей парка была возможность на образовавшиеся уступы помещать различные мелкие предметы. Определите количество цилиндров, которое нужно использовать для создания такой пирамиды, и максимально возможный радиус основания цилиндра, который будет находиться на вершине такой пирамиды.

Входные данные

В первой строке входного файла находится число N – количество цилиндров (натуральное число, не превышающее, 10 000). В следующих N строках находятся значения длин радиусов имеющихся цилиндров (все числа натуральные, не превышающие 10 000), каждое – в отдельной строке. Запишите в ответе два целых числа: сначала количество цилиндров, которое необходимо использовать для строительства пирамиды максимально высоты, затем максимально возможную длину радиуса цилиндра, который можно поместить на вершину такой пирамиды.

Типовой пример организации данных во входном файле

5
53
50
42
50
40

Пример входного файла приведен для пяти цилиндров и случая, когда минимальная допустимая разница между длинами радиусов двух последовательно идущих в пирамиде цилиндров составляет 3 единицы. При таких исходных данных условию задачи удовлетворяют цилиндры с длинами радиусов оснований 40, 50 и 53 или 42, 50 и 53 соответственно, т.е. количество цилиндров равно 3, а радиус верхнего цилиндра составляет 42.

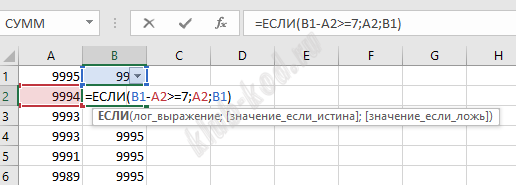
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из файлов, которые идут к сборнику.

Решение и ответ

Решение с помощью электронной таблицы.

Количество строк удалим. Отсортируем таблицу по убыванию. Затем применим формулу =ЕСЛИ(B1-A2>=7;A2;B1), которая будет менять значение в столбце, только если разница между цилиндрами станет равной или больше 7.

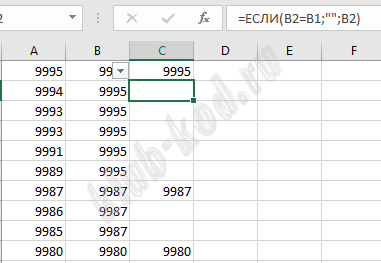
Затем оставим только неповторяющиеся строки.

И посчитаем их количество, что будет ответом на первый вопрос. Ответ на второй вопрос мы найдем в конце таблицы, 2 это и есть наименьший диаметр

Ответ: 1196 2

ВАРИАНТ 2

На прямолинейном участке пути для обеспечения связи необходимо разместить радиопередатчики. Установка каждого такого передатчика возможна на любом из N объектов, включённом в перечень разрешённых. Известно расстояние от нулевой отметки на этом участке до каждого объекта из данного перечня, кроме того по технических нормативам для работы без помех два соседних передатчика должны находиться на расстоянии не менее 6 единиц друг от друга. На данном участке пути необходимо разместить максимальное количество передатчиков, не нарушая технические нормативы. Определите количество передатчиков при таком размещении и максимально возможное расстояние от нулевой отметки до ближайшего к ней передатчика.

Входные данные

В первой строке входного файла находится число N (натуральное число, не превышающее 10 000) - количество объектов, на которых можно устанавливать передатчики. В следующих N строках находятся значения расстояний от нулевой отметки до каждого из этих объектов.

Запишите в ответе два целых числа: сначала максимальное количество передатчиков, которое можно разместить на данном участке пути, не нарушая технические нормативы, затем максимально возможное расстояние от нулевой отметки до ближайшего к ней передатчика при таком размещении.

Типовой пример организации данных в файле

5
63
60
52
60
50

Пример входного файла приведён для пяти объектов установки и случая, когда минимально допустимое расстояние между двумя соседними передатчиками составляет 3 единицы.

При таких исходных данных условию задачи удовлетворяют объекты, расположенные на расстоянии 50, 60 и 63 или 52, 60 и 63 соответственно от нулевой отметки, то есть количество передатчиков равно 3, а расстояние от нулевой отметки до ближайшего к ней передатчика составляет 52.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из файлов, которые идут к сборнику.

Решение и ответ

Решение с помощью электронной таблицы.

Количество строк удалим. Отсортируем таблицу по убыванию. Затем применим формулу =ЕСЛИ(B1-A2>=6;A2;B1), которая будет менять значение в столбце, только если разница между цилиндрами станет равной или больше 7.

Затем оставим только неповторяющиеся строки и посчитаем их количество.

Максимальное расстояние до передатчика найдем в конце таблицы.

Ответ: 489 123

ВАРИАНТ 3

В магазине для упаковки подарков есть N кубических коробок и М декоративных замочков к ним (М < N). Самой интересной считается упаковка подарка по принципу матрёшки - подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т. д., при этом к каждой коробке подбирается подходящий замочек. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 6 единиц меньше длины стороны другой коробки. Замочек подходит к коробке, если маркировка замочка совпадает с длиной стороны коробки. Известно, что коробка, в которой будет находиться подарок, должна быть упакована в синюю коробку. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.

Входные данные

В первой строке входного файла находятся число N - количество коробок в магазине (натуральное число, не превышающее 10 000) и через пробел число М - количество декоративных замочков в магазине (натуральное число, не превышающее 10 000). В следующих M строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000) и через знак табуляции значения, указанные как маркировки на замочках (все числа натуральные, не превышающие 10 000), каждая пара таких значений - в отдельной строке; в последних N - М строках второе число, соответствующее маркировке замочка, опускается, и числа, соответствующие длинам сторон коробок, идут каждое в отдельной строке.

Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.

Типовой пример организации данных во входном файле

5 4
43 40
40 30
32 43
40 31
31

Пример входного файла приведён для случая пяти коробок и четырёх замочков, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрёшкой», составляет 3 единицы.

При таких исходных данных условию задачи удовлетворяют набор коробок с длинами сторон 30, 40 и 43, или 31, 40 и 43 или 32, 40, и 43 т. е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 31 (поскольку замочка для коробки с длиной 32 в магазине нет.

Решение и ответ

f=open('26var03.txt')
st = f.readlines() # создаем массив из строк файла
f.close()
N1,N2 = map (int, st[0].split()) # записываем количество строк в переменную N1, N2
del (st[0]) # удаляем первую строку

A=[]
B=[]
C=[]
D=[]

for i in range(N2):
a, b =map (int, st[i].split()) #разделяем строку на две переменные
A.append(a)
B.append(b)

for i in range(N2,N1):
A.append( int(st[i]) )
A.sort (reverse=True)

for i in A:
for j in B:
if i == j: C.append(i) #Запишем в массив все стороны коробок, для которых есть замочки

x = C[0]
D.append(x)

for i in C:
if x - i >=6:
x = i
D.append(x) #В массив D запишем стороны, удовлетворяющие условию о разнице между длинами сторон

print(len(D), min(D))

Ответ: 585 227

ВАРИАНТ 4

В магазине для упаковки подарков есть N кубических коробок красного, зелёного и синего цвета. Самой интересной считается упаковка подарка по принципу матрёшки - подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т. д., при этом цвета коробок отличаются. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 7 единиц меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.

Входные данные

В первой строке входного файла находится число N - количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000) и через пробел цвет коробки (буква R, G или B).

Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.

Типовой пример организации данных во входном файле

5 4
39 55
40 42
44 44
40 55
50

Пример входного файла приведён для случая пяти коробок красного цвета и четырех коробок синего цвета, когда допустимая разница между длинами сторон коробок, подходящих для упаковки "матрешкой", составляет 3 единицы.

При таких исходных данных условию задачи удовлетворяет набор коробок с длинами сторон 39, 42, 50 и 55 или 40, 44, 50 и 55 соответственно, то есть количество коробок равно 4, а длина стороны самой маленькой коробки 40.

Решение и ответ

Решение моего ученика Егора Курова:
f=open('26var04.txt')
st = f.readlines() # создаем массив из строк файла
f.close()

N1,N2 = map (int, st[0].split()) # записываем количество строк в переменную N1, N2
del (st[0]) # удаляем первую строку

A=[]
B=[]
C=[]

for i in range(N2):
a, b =map (int, st[i].split()) #разделяем строку на две переменные
A.append(a)
B.append(b)

for i in range(N2,N1):
A.append( int(st[i]) )
A.sort (reverse=True)
B.sort (reverse=True)

def ma(b):
for a in A:
if b - a >= 5:
C.append(a)
return mb(a)

def mb (a):
for b in B:
if a - b >= 5:
C.append(b)
return ma(b)

x = max(A[0], B[0])
C.append(x)
if x in B:
ma(x)
else:
mb(x)

print(len(C), min(C))

Ответ: 536 306

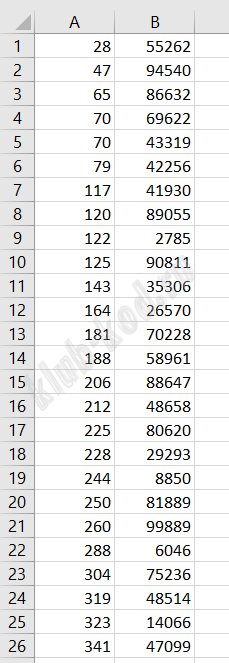
ВАРИАНТ 5

Для хранения двумерного цифрового растрового чёрно-белого изображения Петя сохранил в текстовом файле информацию и позициях всех пикселей чёрного цвета на изображении (номера рядов пикселей и номера чёрных пикселей в ряду). Для редактирования изображения Пете нужно изменить цвет с белого на чёрный всем имеющимся двум соседним белым пикселям, таким что слева и справа от них в том же ряду пиксели чёрные.
Найдите ряд с наибольшим номером, в котором есть два соседних пикселя, удовлетворяющих требованию Пети. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: номер ряда и наименьший номер пикселя в ряду из найденных в этом ряду подходящий пар белых пикселей.

Входные данные

В первой строке входного файла находится число N — количество рядов пикселей (натуральное число, не превышающее 10 000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 100000: номер ряда и номер чёрного пикселя в ряду.

Выходные данные

Два целых неотрицательных числа: номер ряда и наибольший номер пикселя в выбранной паре.

Пример входного файла:
7
20 10
20 13
30 45
40 17
40 20
40 30
40 33

Условию задачи удовлетворяют три пары чисел: 20 и 11, 40 и 18, 40 и 31.

Ответ для приведённого примера: 40 18

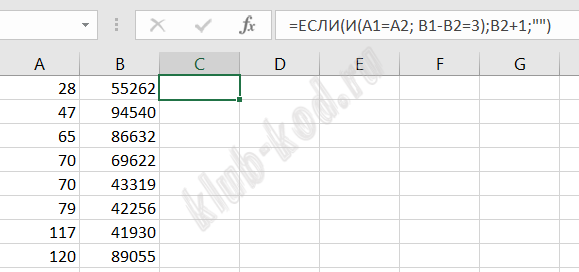
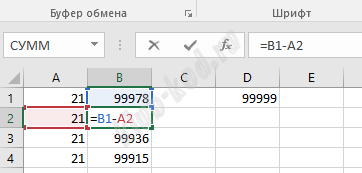
Решение и ответ

Решим задачу с помощью электронной таблицы. Откроем электронную таблицу, в ней откроем текстовый файл с разделителями пробел. Удалим первую строку, содержащую N значений.

Далее применим двухуровневую сортировку: первый столбец по возрастанию, второй по убыванию.

Далее в столбце С запишем формулу с условием И: равенство рядов и разницу между пикселями , равную 3.

Далее применим фильтр, получим непустые строки:

Ответ: 67890 98765

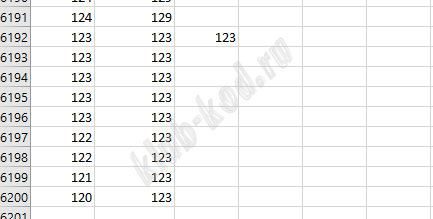
ВАРИАНТ 6

Для хранения двумерного цифрового растрового чёрно-белого изображения Петя сохранил в текстовом файле информацию и позициях всех пикселей чёрного цвета на изображении (номера рядов пикселей и номера чёрных пикселей в ряду). Для редактирования изображения Пете нужно изменить цвет с белого на чёрный всем имеющимся двум соседним белым пикселям, таким что слева и справа от них в том же ряду пиксели чёрные.
Найдите ряд с наименьшим номером, в котором есть два соседних пикселя, удовлетворяющих требованию Пети. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: номер ряда и наибольший номер пикселя в ряду из найденных в этом ряду подходящий пар белых пикселей.

Входные данные

Выходные данные

Два целых неотрицательных числа: номер ряда и наибольший номер пикселя в выбранной паре.

Пример входного файла:
7
30 45
40 17
40 20
40 30
40 33
50 13
50 10
50 13

Условию задачи удовлетворяют три пары чисел: 40 и 19, 40 и 32, 50 и 12.

Ответ для приведённого примера: 40 32

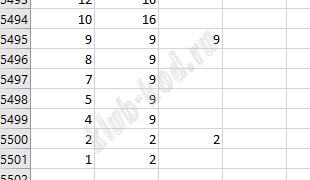
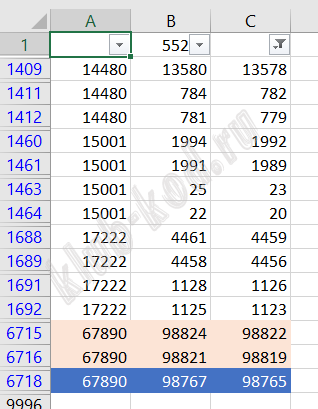
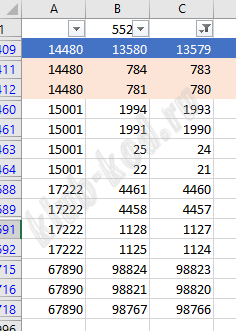
Решение и ответ

Аналогично 5 варианту, только ряд нужно выбрать наименьший, а пиксель наибольший. Поэтому формула примет вид:
=ЕСЛИ(И(A1=A2;B1-B2=3);B1-1;"")

Получим выборку:

Ответ: 14480 13579

ВАРИАНТ 7

Для хранения двумерного цифрового растрового чёрно-белого изображения Петя сохранил в текстовом файле информацию и позициях всех пикселей чёрного цвета на изображении (номера рядов пикселей и номера чёрных пикселей в ряду). Для редактирования изображения Пете нужно изменить цвет с белого на чёрный всем имеющимся трем соседним подряд идущим белым пикселям, таким что слева и справа от них в том же ряду пиксели чёрные.
Найдите ряд с наибольшим номером, в котором есть три соседних пикселя, удовлетворяющих требованию Пети. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: номер ряда и наименьший номер пикселя в ряду из найденных в этом ряду подходящий троек белых пикселей.

Входные данные

Выходные данные

Два целых неотрицательных числа: номер ряда и наибольший номер пикселя в выбранной тройке.

Пример входного файла:
7
20 10
20 14
30 45
40 17
40 21
40 30
40 34

Условию задачи удовлетворяют три пары чисел: 20 и 11, 40 и 18, 40 и 31.

Ответ для приведённого примера: 40 18.

Решение и ответ

Аналогично 5 варианту, только в формуле разница между черными пикселями равна 4.

=ЕСЛИ(И(A1=A2;B1-B2=4);B2+1;"")

Ответ: 78950 55774

ВАРИАНТ 8

Для хранения двумерного цифрового растрового чёрно-белого изображения Петя сохранил в текстовом файле информацию и позициях всех пикселей чёрного цвета на изображении (номера рядов пикселей и номера чёрных пикселей в ряду). Для редактирования изображения Пете нужно изменить цвет с белого на чёрный всем имеющимся трем соседним белым пикселям, таким что слева и справа от них в том же ряду пиксели чёрные.
Найдите ряд с наименьшим номером, в котором есть три соседних пикселя, удовлетворяющих требованию Пети. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: номер ряда и наибольший номер пикселя в ряду из найденных в этом ряду подходящий пар белых пикселей.

Входные данные

Выходные данные

Два целых неотрицательных числа: номер ряда и наибольший номер пикселя в выбранной паре.

Пример входного файла:
7
30 45
40 17
40 21
40 30
40 34
50 10
50 14

Условию задачи удовлетворяют три пары чисел: 40 и 20, 40 и 33, 50 и 13.

Ответ для приведённого примера: 40 33

Решение и ответ

Аналогично варианту 6

Ответ: 12876 19283

ВАРИАНТ 9

Илье необходимо перенести файлы с одного компьютера на другой при помощи внешнего жёсткого диска.
Объём диска может быть меньше, чем требуется для переноса файлов за один раз. Свободный объём на диске и размеры файлов известны.
По заданной информации об объёме файлов на компьютере и свободном объёме на диске определите максимальное число файлов, которые могут быть перенесены за один раз на внешний жесткий диск, а также максимальный размер файла, записанного на этот диск, при условии, что перенесено наибольшее возможное число файлов.

Входные данные
В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превосходящее 100000) и N — количество файлов, которые надо перенести (натуральное число, не превышающее 10000). В следующих N строках находятся значения обьемов указанных файлов (все числа натуральные, не превышающие 100), каждое в отдельной строке.

Выходные данные
Запишите в ответе два числа: сначала наибольшее число файлов, которые могут быть перенесены на внешний жёсткий диск за один раз, затем максимальный размер перенесённого файла, при условии, что перенесено наибольшее возможное число файлов. Если вариантов переноса несколько, выберите тот, при котором будет перенесён наибольший файл.

Пример входного файла:
100 4
80
30
50
40

При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов: 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера: 2 50.

Решение и ответ

Решение с помощью электронной таблицы.

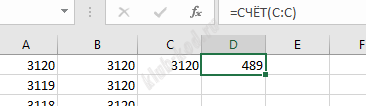
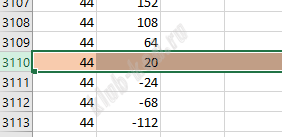
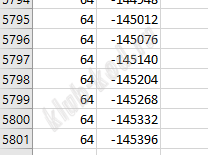
Значения S перенесем в ячейку D1 и удалим. Отсортируем таблицу по возрастанию. Затем будем считать оставшееся место на диске при условии что хотим записать наибольшее число файлов.

B1=99999-A1
B2 = B1 - A2

Найдем строку, в которой закончилось место на диске.

Мы видим, что поместилось 3110 файлов и осталось место 20. заменим последний файл на файл, размером 64 при условии что такой существует в списке.

Ответ: 3110 64

ВАРИАНТ 10

Входные данные
В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превосходящее 100000) и N — количество файлов, которые надо перенести (натуральное число, не превышающее 10000). В следующих N строках находятся значения обьемов указанных файлов (все числа натуральные, не превышающие 100), каждое в отдельной строке.

Пример входного файла:
100 4
80
30
50
40

При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов: 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера: 2 50.

Решение и ответ

Аналогично варианту 9

Ответ: 3098 80

Добавить комментарий

JComments

Rating:

( 1 Rating )

Задание 26. Обработка целочисленной информации

РСЯ футер