Перестановки
Перестановкой называется конечное множество, в котором установлен порядок элементов.
Формула количества перестановок (Сколькими способами можно переставить n объектов?)
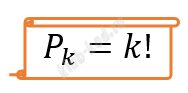 |
Пример 1. Дано:
 |
Сколько существует способов переставить ягоды местами?
Решение: P3 = 3! = 1 ⋅ 2 ⋅ 3 = 6 (см. рисунок "Перестановки")
 |
Ответ: 6
Пример 2. В команде 6 человек. Сколькими способами они могут выстроиться для приветствия?
Решение: P6 = 6! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 = 720 вариантов приветствия
Ответ: 720
Пример 3. Имеется 10 различных книг, среди которых есть трёхтомник одного автора. Сколькими способами можно расставить эти книги на полке, если книги трёхтомника должны находиться вместе, но в любом прядке?
Решение: Поскольку книги трехтомника должны стоять рядом, то будем считать его за 1 книгу. И поскольку в любом порядке, то здесь идет речь о произведении перестановок.
P8 ⋅ P3 = 8! ⋅ 3!= 241920 вариантов перестановок книг.
Перестановки с повторениями
Дано: множество, состоящее из объектов, среди которых есть одинаковые (либо считающиеся таковыми по смыслу задачи).
Формула количества перестановок с повторениями (Количество способов, которыми можно переставить n объектов, среди которых 1-й объект повторяется n1 раз, 2-й объект повторяется n2 раз, 3-й объект – n3 раз,…, k -й объект – nk раз, n = n1 + n2 + ... + nk)
 |
Если имеются неповторяющиеся объекты, в этом случае соответствующие значения n равны единице.
Пример 1. Алексей занимается спортом. 4 раза в неделю - легкой атлетикой, 2 раза в неделю силовыми упражнениями и один день отдыхает. Сколькими способами он может составить себе расписание на неделю?
Решение: Имеем набор {л л л л с с о}. Имеем набор семиэлементного множества 7!, но мы не должны учитывать перестановки, в которых одинаковые элементы меняются местами, поэтому должны поделить на 4! ⋅ 2!
Р7= 7! / (4! ⋅ 2!) = 105.
Ответ: 105
Пример 2. Сколько слов можно составить, переставив буквы в слове «экзамен», в слове «математика», в слове «колобок»?
Решение:
"Экзамен" – 7 букв ( без повторений), поэтому Р7 = 7! = 5040
"Математика" - 10 букв (м-2, а-3, т-2, е-1, и-1, к-1), перестановки с повторениями Р10= 10! / (2! ⋅ 3! ⋅ 2! ⋅ 1! ⋅ 1! ⋅ 1! ) = 151200
"Колобок" - 7 букв (к-2, о-3, л-1, б-1) , перестановки с повторениями Р7= 7! / (2! ⋅ 3!) = 420
Ответ: 5040; 151200; 420
Сочетания
Подмножества, составленные из n элементов данного множества и содержащие k элементов в каждом подмножестве, называют сочетаниями из n элементов по k. (Сочетания различаются только элементами, порядок их не важен: ab и ba – это одно и тоже сочетание).
Формула количества сочетаний (Сколькими способами можно выбрать k объектов из n ?)
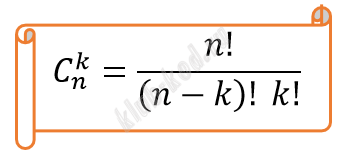 |
Пример 1. Дано:
 |
Сколько существует способов выбрать из трех ягод по две?
Решение: С32= 3! /( 1! ⋅ 2!) = 3 (см. рисунок "Сочетания")
 |
Ответ: 3
Пример 2. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
Решение: С72 =7! /(2! ⋅ (7 - 2)!) = 7! /(2! ⋅ 5!) = (6 ⋅ 7)/2 = 21
Ответ: 21
Пример 3. На тренировках занимаются 12 баскетболистов. Сколько может быть организовано тренером разных стартовых пятерок?
Решение: С125 =12! /(5! ⋅ (12 - 5)!) = 12! /(5! ⋅ 7!) = (12 ⋅ 11 ⋅ 10⋅ 9⋅ 8 ⋅ 7!)/(5! ⋅ 7!) = (12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8) /120 = 11⋅ 9⋅ 8 = 792
Ответ: 792
Пример 4. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?
Решение: Т.к. двое мальчиков войдут в команду, то остается отобрать 3 из 8. Для выборки важен только состав (по условию все члены команды не различаются по ролям).
С83 = 8! /(3! ⋅ (8 - 3)!) = 8! /(3! ⋅ 5!) = (8 ⋅ 7 ⋅ 6 ⋅ 5!)/(3! ⋅ 5!) = (8 ⋅ 7 ⋅ 6) / 6 = 56
Ответ: 56.
Пример 5. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?
Решение: В одной игре участвуют 2 человека, следовательно, нужно вычислить, сколькими способами можно отобрать 2-х человек из 15, причем порядок в таких парах не важен.
С152 = 15! /(2! ⋅ (15 - 2)!) = 15! /(2! ⋅ 13!) = (15 ⋅ 14 ⋅ 13!)/(2! ⋅ 13!) = (15 ⋅ 14) / 2 = 105
Ответ: 105.
Сочетания с повторениями
Формула количества сочетаний с повторениями (Сколькими способами можно выбрать k объектов в множестве, состоящем из n элементов, причем элементы возвращаются обратно?)
Здесь в выборке могут оказаться одинаковые объекты, и если k > n , то совпадения точно будут. По умолчанию предполагается, что исходная совокупность содержит не менее k объектов каждого вида, и поэтому выборка может полностью состоять из одинаковых объектов.
 |
Пример 1. Дано:
 |
Сколько существует способов выбрать с повторениями из трех ягод по две?
Решение: С3(повт)2= С42= 4! /( 1! ⋅ 2!) = 6 (см. рисунок "Сочетания с повторениями")
 |
Ответ: 6
Пример 2. В кошельке находится достаточно большое 1 -рублевых, 2-х, 5-ти и 10-и рублёвых монет. Сколькими способами можно извлечь три монеты из кошелька?
Решение: Используя формулу количества сочетаний с повторениями, получаем:
С4(повт)3 = С63 = 6! /(3! ⋅ (4 - 1)!) = 6! /(3! ⋅ 3!) = (6 ⋅ 5 ⋅ 4 ⋅ 3!)/(3! ⋅ 3!) = (6 ⋅ 5 ⋅ 4) / 6 = 20 способами можно выбрать 3 монеты из кошелька.
Ответ: 20.
Пример 3: В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить 12 открыток для поздравлений?
Решение: С10(повт)12 = С2112 = 21! /(12! ⋅ (21 - 12)!) = 21! /(12! ⋅ 9!) = (21 ⋅ 20 ⋅ 19 ⋅ 18 ⋅ 17 ⋅ 16 ⋅ 15 ⋅ 14 ⋅ 13 ⋅ 12!)/(12! ⋅ 9!) =(21 ⋅ 20 ⋅ 19 ⋅ 18 ⋅ 17 ⋅ 16 ⋅ 15 ⋅ 14 ⋅ 13)/(3 ⋅ 18 ⋅ 21 ⋅ 20 ⋅ 16) = 19 ⋅ 17 ⋅ 5 ⋅ 14 ⋅ 13 = 293930
Ответ: 293930.
Размещения
Размещением из n элементов по k (k≤n) называется любое множество, состоящее из k элементов, взятых в определённом порядке из данных n элементов.
Формула количества размещений (Сколькими способами можно выбрать k объектов из n и в каждой выборке переставить их местами, либо распределить между ними какие-нибудь уникальные атрибуты?)
 |
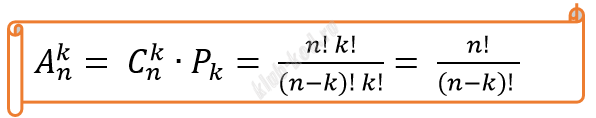 |
Пример 1. Дано:
 |
Сколько существует размещений из трех ягод по две?
Решение: А32= 3! / 1! = 6 (см. рисунок "Размещения")
 |
Ответ: 6
Пример 2. Сколько трехзначных чисел можно составить из цифр 2, 4, 6, 7, 9?
Решение: А53 = 5! /(5 - 3)! = 5! /2! = 120/2 = 60
Ответ: 60.
Пример 3. В соревнованиях высшей лиги по футболу участвуют 18 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами могут быть распределены медали между командами?
Решение: А183 = 18! /(18 - 3)! = 18! /15! = 18 ⋅ 17 ⋅ 16 = 4896
Ответ: 4896.
Пример 4. Даниэль составляет коды из букв слова ДАНИЭЛЬ . Код должен состоять из 10 букв, он не может начинаться с буквы Ь и должен содержать все гласные буквы ровно по одному разу. Сколько различных кодов может составить Даниэль?
Решение: 1) Сначала найдем все возможные варианты таких слов, не ограничивая и считая мягкий знак согласной:
Найдем количество размещений гласных букв в 10-и позициях: А103 = 10! /(10 - 3)! = 10! /7! = 10 ⋅ 9 ⋅ 8 = 720
Умножим размещения гласных на остальные варианты семи позиций согласных букв: А103 ⋅ 47 = 11 796 480
2) Из всех вариантов вычтем слова, начинающиеся с Ь:
Гласные в этом случае будут размещаться на 3-х из 9-и позиций: А93 = 9! /(9 - 3)! = 9! /6! = 9 ⋅ 8 ⋅ 7 = 504
Умножим размещения гласных на остальные варианты шести позиций четырех согласных букв: А93 ⋅ 46 = 2 064 384
3) Из 1) Вычтем слова найденные в пункте 2):
11 796 480 - 2 064 384 = 9 732 096
Ответ: 9 732 096
Пример 5. Николай составляет коды из букв слова НИКОЛАЙ. Код должен состоять из 11 букв, он не может начинаться с буквы Й и должен содержать все гласные буквы ровно по одному разу. Сколько различных кодов может составить Николай?
Решение: 1) Сначала найдем все возможные варианты таких слов, не ограничивая и считая Й:
Найдем количество размещений гласных букв в 11-и позициях: А113 = 11! /(11 - 3)! = 11! /8! = 11 ⋅ 10 ⋅ 9 = 990
Умножим размещения гласных на остальные варианты восьми позиций четырех согласных букв: А113 ⋅ 48 = 990 ⋅ 65 536 = 64 880 640
2) Из всех вариантов вычтем слова, начинающиеся с Й:
Гласные в этом случае будут размещаться на 3-х из 10-и позиций: А103 = 10! /(10 - 3)! = 10! /7! = 10 ⋅ 9 ⋅ 8 = 720
Умножим размещения гласных на остальные варианты семи позиций четырех согласных букв: А103 ⋅ 47 = 720 ⋅ 16 384= 11 796 480
3) Из 1) Вычтем слова найденные в пункте 2):
64 880 640 - 11 796 480 = 53 084 160
Ответ: 53 084 160
Размещения с повторениями
Дано множество, состоящее из n объектов, при этом любой объект можно выбирать неоднократно. Сколькими способами можно выбрать k объектов, если важен порядок их расположения в выборке? В частности, возможен случай, когда из n имеющихся объектов k раз будет выбран какой-то один объект.
Формула количества размещений с повторениями (Сколькими способами можно выбрать k объектов, если важен порядок их расположения в выборке?)
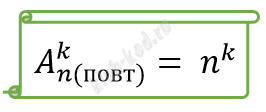 |
Пример 1. Дано:
 |
Сколько существует способов разместить с повторениями из трех ягод по две?
Решение: А3(повт)2 = 32= 9
 |
Ответ: 9
Пример 2. Согласно государственному стандарту, автомобильный номерной знак состоит из 3 цифр и 3 букв. При этом недопустим номер с тремя нулями, а буквы выбираются из набора А, В, Е, К, М, Н, О, Р, С, Т, У, Х (используются только те буквы кириллицы, написание которых совпадает с латинскими буквами). Сколько различных номерных знаков можно составить для региона?
Решение:
А10(повт)3 = 103 = 1000 –способами можно составить цифровую комбинацию автомобильного номера, при этом одну из них (000) следует исключить А10(повт)3 - 1 = 999
А12(повт)3 = 123 = 1728 – способами можно составить буквенную комбинацию автомобильного номера.
По правилу умножения комбинаций, всего можно составить: А10(повт)3 ⋅ А12(повт)3 = 999 ⋅ 1728 = 1 726 272 автомобильных номера для региона.
Ответ: 1 726 272.
Пример 3. Человек, пришедший в гости, забыл код, открывающий дверь подъезда, но помнил, что он составлен из нулей и единиц и всего имеет четыре цифры. Сколько вариантов кода в худшем случае ему придётся перебрать, чтобы открыть дверь?
Решение: А2(повт)4 = 24 = 16
Ответ: 16.
Пример 4. Каких чисел от 1 до 1 000 000 больше: тех, в записи которых встречается единица, или тех, в которых она не встречается?
Решение: Подсчитаем количество чисел от 1 до 999999 в записи которых нет единиц. Каждую цифру можно выбрать 9 способами (любая цифра кроме 1), поэтому все 6 цифр можно выбрать 96 способами. При этом один вариант (000000) нужно убрать, так как число 0 не рассматривается. Получаем всего 96 − 1 = 531 440 чисел. Так как всего чисел 1 000 000, то видно, что чисел без единицы среди чисел от 1 до 1 000 000 больше, чем тех, в записи которых единица есть.
Ответ: чисел без единицы больше.



