|
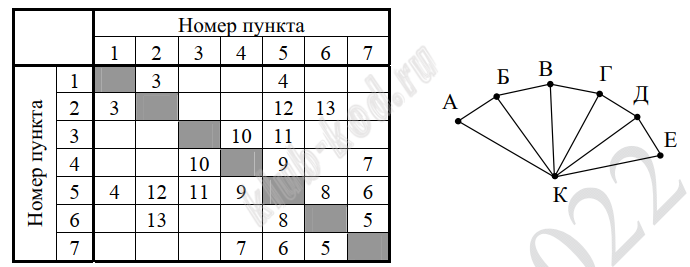
Задание 1. Анализ информационных моделей На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта Б в пункт В и из пункта Г в пункт Д. В ответе запишите целое число.
|
Решение и ответ Анализируя расположение дорог в графе, можно предположить два варианта расположения вершин в таблице. Поскольку искомые дороги симметричны, сумма дорог получится одинаковой в обоих случаях.
Ответ: 20 |
||||||||||||||||||||||||||||||||||||
|
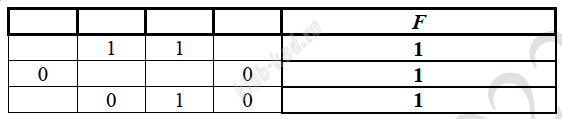
Задание 2. Построение таблиц истинности логических выражений Миша заполнял таблицу истинности функции F= ¬(y → (x≡w)) & (z→ x), но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx.
|
Решение и ответ Сделаем преобразования по законам логики и составим таблицу истинности для выражения y & ¬(x ≡ w) & (z → x).
У нас 4 логические переменные х, y, z, w, то есть получим 24 набора логических значений. Среди всех найдем те наборы, удовлетворяют выражению. Получим:
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности. F это конъюнкция трех выражений и она равна 1, значит столбец y может содержать только 1. То есть это третий столбец. Далее мы видим, что набор (1, 1, 1, 0) может быть только в первой строке. Заполним вторую строку 0 1 1 0 и третью 1 0 1 0 согласно наборам. Поскольку z → x = 1, то z это четвертый столбец, а x второй. Ответ: WXYZ |
||||||||||||||||||||||||||||||||||||
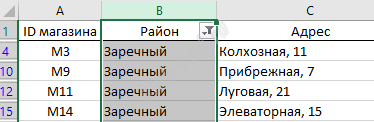
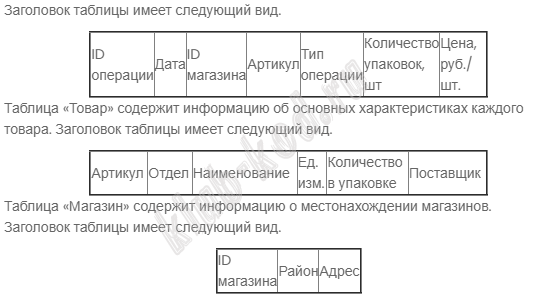
Задание 3. Базы данных. Файловая система В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в
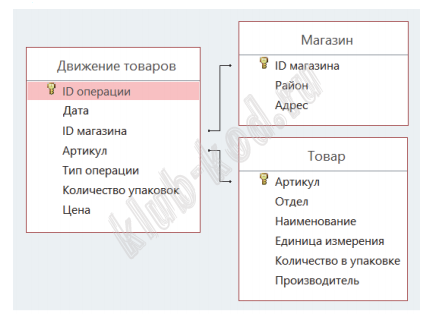
На рисунке приведена схема указанной базы данных. |
Решение и ответ На третьем листе книги применим фильтр по району и получим ID четырех магазинов.
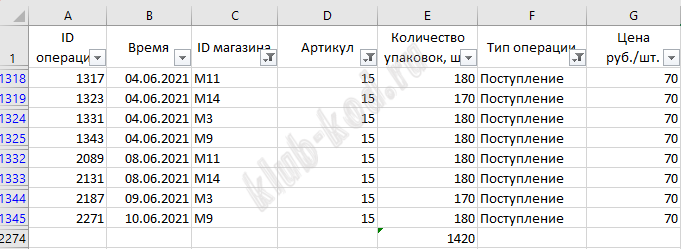
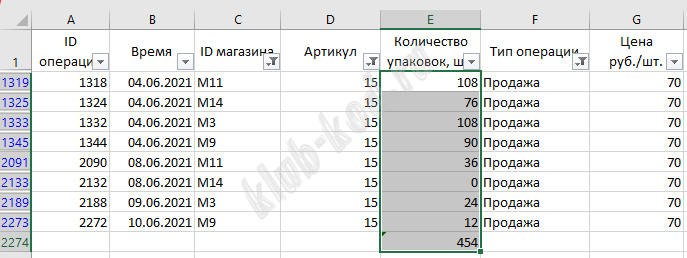
На втором листе применим фильтр по товару и получим ID товара.
На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 10 июня. Получим: Поступило в продажу 1420 упаковок. Продано 454. Разница и есть искомый ответ 1420-454=966 Ответ: 966 |
||||||||||||||||||||||||||||||||||||
|
Задание 4. Кодирование и декодирование информации Для кодирования некоторой последовательности, состоящей из букв Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся букв – П и Р – кодовые слова неизвестны. Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с наименьшим числовым значением. |
Решение и ответ Поскольку никакое кодовое слово не является началом другого кодового слова, код 10 использовать нельзя, значит получим два слова 100 и 101, из которых наименьшее 100 и будет ответом на вопрос задачи.
Ответ: 100 |
||||||||||||||||||||||||||||||||||||
|
Задание 5. Анализ и построение алгоритмов для исполнителей На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1. Строится двоичная запись числа N. 2. К этой записи дописываются справа ещё два разряда по следующему правилу: а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления. |
Решение и ответ Минимальное R, большее 77, это 78.
Мы видим, что подходят по алгоритму числа 78 и 80, из которых 78 наименьшее. Чтобы найти искомое число N, отбросим два дополнительных разряда от найденного 1001110. Правило: Если от двоичного числа отбросить младший разряд, то оно разделится на 2 целочисленным образом (т.е. делим на 2, если есть остаток, убираем его). Уберём второй дополнительный разряд у числа 1001110, получается 78 / 2 = 39 (100111). Уберём ещё и первый дополнительный разряд , получается 39 / 2 = 19 (10011), следовательно двоичное представление искомого числа N равно 10011, а десятичное 19. Ответ: 19 |
||||||||||||||||||||||||||||||||||||
|
Задание 6. Анализ программ Определите, при каком наибольшем введённом значении переменной s программа выведет число 64.s = int(input()) |
Решение и ответ Переменная n менялась в цикле от 1 до 64, на каждом шаге, увеличивалась в 2 раза. Построим трассировочную таблицу в обратном порядке.
Наибольшее значение s на первом шаге равно 259. Обратный алгоритм Рython n = 64 Ответ: 259 |
||||||||||||||||||||||||||||||||||||
|
Задание 7. Кодирование и декодирование информации. Передача информации Для хранения произвольного растрового изображения размером 128×320 пикселей отведено 20 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении? |
Решение и ответ N = 2 i, I = K · i , i = I/K I = 20 · 213 бит К = 27 · 25 · 10 = 5 · 213 i = (20 · 213)/ (5 · 213) = 4 бита N = 24 = 16 символов Ответ: 16 |
||||||||||||||||||||||||||||||||||||
|
Задание 8. Перебор слов и системы счисления Все четырёхбуквенные слова, в составе которых могут быть только буквы Л, Е, М, У, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1. Ниже приведено начало списка. |
Решение и ответ {Л, Е, М, У, Р}. На каждом из четырех мест четырехбуквенного слова Буквы расположены по алфавиту. Л после Е. Значит слово, Ответ: 126 |
||||||||||||||||||||||||||||||||||||
Задание 9. Работа с таблицами Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел может являться сторонами треугольника, то есть удовлетворяет неравенству треугольника. В ответе запишите только число. |
Решение и ответ Согласно неравенству треугольника каждая сторона долна быть меньше суммы двух других сторон. В ячейку Е1 введем формулу: =ЕСЛИ(И(A1<B1+C1;B1<A1+C1;C1<A1+B1);1;0) и скопируем её во все ячейки диапазона E2:E5000. Затем найдем сумму всех ячеек столбца Е. Получим 2453.
Ответ: 2453 |
||||||||||||||||||||||||||||||||||||
Задание 10. Поиск символов в текстовом редакторе С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «долг» или «Долг» в тексте романа в стихах А. С. Пушкина «Евгений Онегин». Другие формы слова «долг», такие как «долги», «долгами» и т. д., учитывать не следует. В ответе укажите только число. |
Решение и ответ
В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Оно встречается один раз во фразе "Цензуре долг свой заплачу".
Ответ: 1 |
||||||||||||||||||||||||||||||||||||
|
Задание 11. Вычисление количества информации При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 8-символьного набора: А, В, C, D, Е, F, G, H. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 24 байт на одного пользователя. Определите объём памяти (в байтах), необходимый для хранения сведений о 20 пользователях. В ответе запишите только целое число — количество байт. |
Решение и ответ N : { А, В, C, D, Е, F, G, H} – всего 8 различных символов в наборе N = 2 i, 8=23, значит для кодирования одного символа нужно 3 бита I = K · i I = 15 · 3 = 45 бит ≈ 6 байт – отводится на пароль I = 6 + 24 = 30 байт – на одного пользователя (с доп. информацией) I20 = 20 · 30 = 600 байт – всего Ответ: 600 |
||||||||||||||||||||||||||||||||||||
|
Задание 12. Выполнение алгоритмов для исполнителей Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется. Цикл выполняется, пока условие истинно. В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно). В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно). Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 70 идущих подряд цифр 8? В ответе запишите полученную строку. НАЧАЛО |
Решение и ответ
s = 70 * '8' print(s) while "2222" in s or "8888" in s: if "2222" in s: s = s.replace( "2222", "88", 1 ) print(s) else: s = s.replace( "8888", "22", 1 ) print(s) 35 раз каждые четыре символа будут заменены на два. Останется 22
Ответ: 22 |
||||||||||||||||||||||||||||||||||||
|
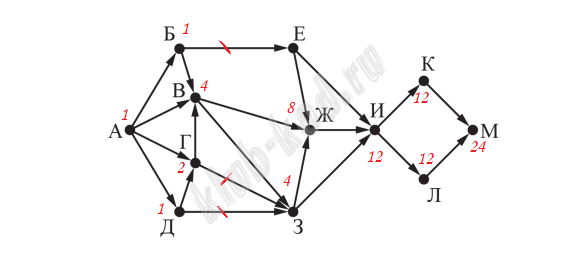
Задание 13. Поиск путей в графе На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.Сколько существует различных путей из города А в город М, проходящих через город В?
|
Решение и ответ
Ответ: 24 |
||||||||||||||||||||||||||||||||||||
|
Задание 14. Кодирование чисел. Системы счисления Значение арифметического выражения 3 · 438 + 2 · 423 + 420 + 3 · 45 + 2 · 44 + 1 записали в системе счисления с основанием 16. Сколько значащих нулей содержится в этой записи?
|
Решение и ответ 3 · 438 + 2 · 423 + 420 + 3 · 45 + 2 · 44 + 1 = 3 · 1619 + 8 · 1611 + 1 · 1610 + 12 · 162 + 2 · 162 + 1 · 160 = 3 · 1619 + 8 · 1611 + 1 · 1610 + 14 · 162 + 1 · 160 = 30000000810000000Е01 В развернутой форме записи числа получится всего 20 цифр, из которых 5 не нули. Решение на python x=3*4**38 + 2 *4**23 + 4**20 + 3*4**5 + 2*4**4+1 Ответ: 15 |
||||||||||||||||||||||||||||||||||||
|
Задание 15. Преобразование логических выражений На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение(x ∈ D) → ((¬(x ∈ C) & ¬(x ∈ A)) → ¬(x ∈ D)) истинно (т.е. принимает значение 1) при любом значении переменной х.
|
Решение и ответ 
Ответ: 12 |
||||||||||||||||||||||||||||||||||||
|
Задание 16. Рекурсивные алгоритмы Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями: F(n) = 1 при n = 1; F(n) = n + F(n − 1), если n — чётно; F(n) = 2 × F(n − 2), если n> 1 и при этом n — нечётно. Чему равно значение функции F(26)?
|
Решение и ответ F(1) = 1
Мы видим, что значения функции от нечетных n представляют из себя степени двойки. F(26) = 26 + F(25) = 26 + 212 = 26 + 4096 = 4122 Решение на Python def F(n): Ответ: 4122 |
||||||||||||||||||||||||||||||||||||
Задание 17. Проверка на делимость В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых хотя бы одно число делится на 3, а сумма элементов пары не более максимального элемента последовательности, кратного 3. В ответе запишитеколичество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
|
Решение и ответ with open("17.txt", "r") as f: #читаем файл k=0 Ответ: 2802 1990 |
||||||||||||||||||||||||||||||||||||
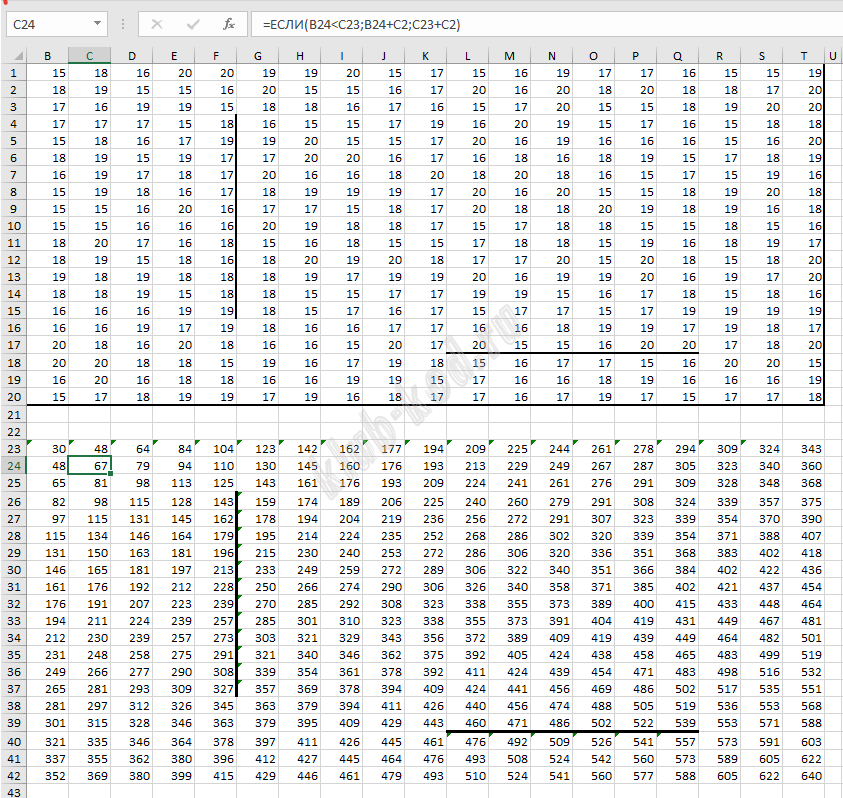
Задание 18. Робот-сборщик монет Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел 41 и 22. |
Решение и ответ Найдём максимальную денежную сумму. Для этого найдём максимальную денежную сумму для каждой ячейки таблицы. В ячейку AA1 запишем формулу =СУММ($A$1:A1). Скопируем эту формулу во все ячейки в диапазоне AA1:AT1 и в диапазоне AA2:AA20. Для остальных ячеек будем сравнивать значение ячейки слева и значение ячейки сверху и присваивать текущей ячейке значение суммы той ячейки, в которой значение больше, и текущей ячейки. В AB2 запишем формулу =ЕСЛИ(AA2>AB1;AA2+B2;AB1+B2) и скопируем эту формулу во все ячейки диапазона AB2:AT20. Справа от первой стены изменим формулу =AG3+G4 и протянем вниз до конца стены. Снизу от второй стены в ячейке AL18 изменим формулу =AK18+L18 и протянем вправо до конца стены.
Таким образом, в ячейке AT20 получим значение максимальной денежной суммы — 721. Аналогичным образом найдём значение минимальной денежной суммы. Ячейки диапазонов А23:Е23 и А23:А42 заполняются также, как при поиске максимальной денежной суммы. В В24 запишем формулу ЕСЛИ(A24<B23;A24+B2;B23+B2) и скопируем эту формулу во все ячейки диапазона В24:Т24. Справа от первой стены в ячейке G26 изменим формулу =G25+G4 и протянем вниз до конца стены. Снизу от второй стены в ячейке L40 изменим формулу =AK18+L18 и протянем вправо до конца стены.
Таким образом, в ячейке Т24 получим значение минимальной денежной суммы — 640. Ответ: 721 640 |
||||||||||||||||||||||||||||||||||||
|
Задание 19. Выигрышная стратегия. Задание 1 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 28. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. |
Решение и ответ При значениях S < 14 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 14 Петя своим первым ходом может получить 15 или 28 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом. Ответ: 14 |
||||||||||||||||||||||||||||||||||||
|
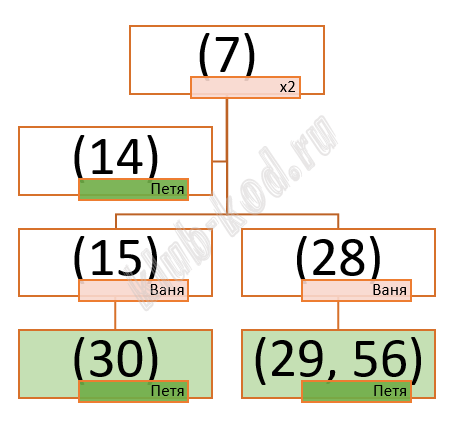
Задание 20. Выигрышная стратегия. Задание 2 Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
Найденные значения запишите в порядке возрастания. |
Решение и ответ Значение S должно быть меньше 14, поскольку иначе Ваня сможет выиграть своим первым ходом.
Ответ: 7 13 |
||||||||||||||||||||||||||||||||||||
|
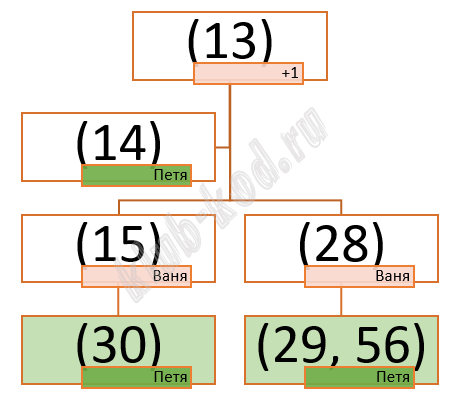
Задание 21. Выигрышная стратегия. Задание 3 Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:
Если найдено несколько значений S, в ответе запишите минимальное из них. |
Решение и ответ Ответ: 12 |
||||||||||||||||||||||||||||||||||||
|
Задание 22. Анализ программы с циклами и условными операторами Дан алгоритм. (код на языке Python). Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 4, а потом 5. x = int(input()) Q = 9 L = 0 while x >= Q: L = L + 1 x = x - Q M = x if M < L: M = L L = x print(L) print(M) |
Решение и ответ Данный алгоритм ищет два числа: целую часть от деления x на 9 и остаток от деления x на 9. Если остаток от деления числа x на 9 меньше, чем целая часть, то алгоритм меняет местами значения L и M. В результате работы алгоритма на экран будут выведены два числа: 4 и 5. Значит, чтобы найти наибольшее число x, число 5 должно являться целой частью от деления x на 9, а число 4 — остатком от деления x на 9. То есть, x = 9 · 5 + 4 = 49. Решение на Python def f(x): x = 1 Ответ: 49 |
||||||||||||||||||||||||||||||||||||
|
Задание 23. Анализ программы с циклами и условными операторами Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера: 1. Прибавить 1 Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя — это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 20 и при этом траектория вычислений содержит число 10? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17. |
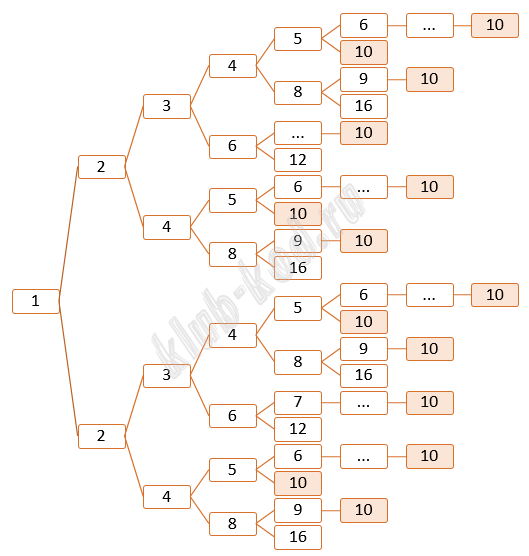
Решение и ответ
Данное дерево вариантов показывает программы получения 10 из 1. Всего мы видим 14 различных вариантов. Чтобы получить из числа 10 число 20, есть два варианта, То есть 14 * 2 = 28 Решение на Python def f(x, y): print (f(1,10) * f(10, 20)) Ответ: 28 |
||||||||||||||||||||||||||||||||||||
Задание 24. Анализ программы с циклами и условными операторами Текстовый файл состоит из символов P, Q, R и S. Определите максимальное количество идущих подряд символов в прилагаемом файле, среди которых нет идущих подряд символов P. Для выполнения этого задания следует написать программу.
|
Решение и ответ with open("24.txt", "r") as f: s=f.readline() #читаем файл в массив m=k=1 #счетчик и максимальный набор идущих подряд символов приравниваем 1 for i in range(2, len(s)): if s[i]!='P' or s[i-1]!='P': #проверяем, чтобы два Р не стояли рядом print(m) Ответ: 188 |
||||||||||||||||||||||||||||||||||||
|
Задание 25. Анализ программы с циклами и условными операторами Пусть M – сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей у числа нет, то значение M считается равным нулю. Напишите программу, которая перебирает целые числа, бо́льшие 700 000, в порядке возрастания и ищет среди них такие, для которых значение M оканчивается на 8. Выведите первые пять найденных чисели соответствующие им значения M. Формат вывода: для каждого из пяти таких найденных чисел в отдельной строке сначала выводится само число, затем – значение М. Строки выводятся в порядке возрастания найденных чисел. Количество строк в таблице для ответа избыточно.
|
Решение и ответ k=0 n=700001 while k<5: #ограничиваем количество чисел M=0 for i in range(2,n):#перебираем делители пока не найдем минимальный и прерываем цикл if n%i==0: M = i + n/i #минимальный и максимальный делители в паре break if M%10==8: #проверяем последнюю цифру k+=1 print (n, int(M)) #вывод на печать n+=1 Ответ: |
||||||||||||||||||||||||||||||||||||
Задание 26. Анализ программы с циклами и условными операторами Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя. По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей. В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 10 000) и N — количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке. Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей. Пример входного файла: 100 4 При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера: 2 50 |
Решение и ответ f = open("26.txt", "r") st=f.readline().split() S=int(st[0]) # размер свободного места на диске N=int(st[1]) # количество пользователей I=0 # объем файлов пользователей del(st) P=[int(i) for i in f] # массив файлов пользователей P.sort() #сортируем по возрастанию k=0 #количество файлов, которые смогут поместиться на диске for i in P: m=0 # максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей for i in range(len(P)): print(k,m) Ответ: 568 50 |
||||||||||||||||||||||||||||||||||||
Задание 27. Анализ программы с циклами и условными операторами Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой Входные данные Файл А Пример организации исходных данных во входном файле: Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго. |
Решение и ответ Для файла А публикую алгоритм методом перебора.
with open("27_A.txt", "r") as f: for i in range (len(p)): # читаем массив по переменной i for j in range (i+1,len(p)): # читаем массив по j print (ms,d) Решение для 2-х файлов f=open('27_B.txt') N = p[0] #количество элементов в массиве for i in range(N): print(l) Ответ: 185 844158 |
||||||||||||||||||||||||||||||||||||
В решение заданий демо-версии используется язык программирования Python.
- Разбор демо-версий
- Просмотров: 6751






 Используя информацию из приведённой базы данных, определите на сколько увеличилось количество упаковок яиц диетических, имеющихся в наличии в магазинах Заречного района, за период с 1 по 10 июня включительно. В ответе запишите только число.
Используя информацию из приведённой базы данных, определите на сколько увеличилось количество упаковок яиц диетических, имеющихся в наличии в магазинах Заречного района, за период с 1 по 10 июня включительно. В ответе запишите только число.