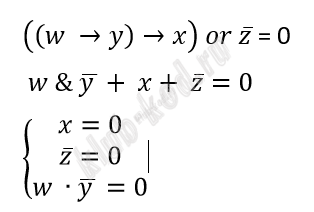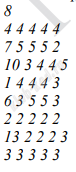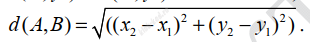|
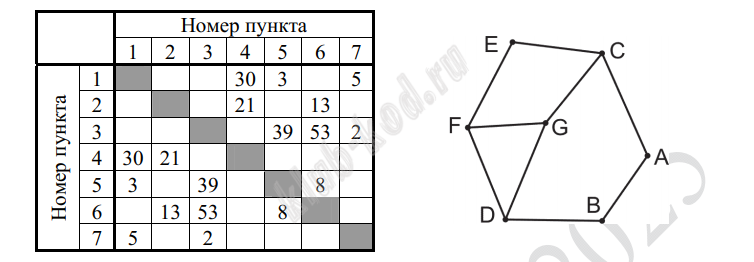
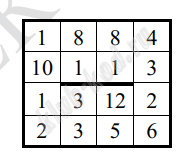
Задание 1. Анализ информационных моделей На рисунке изображена схема дорог N-ского района. В таблице звездочкой обозначено наличие дороги из одного населенного пункта в другой.
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт G и из пункта A в пункт C. В ответе запишите целое число. |
Решение и ответ Анализируя таблицу и граф, расставим веса вершин. Это двойки и тройки. Найдем уникальную вершину. Это вершина Е, которая соединена с двумя вершинами тройками, 1 и 3, далее находим из них ту, что выходит на двойку, то есть на А. Значит С это 1, а F это 3. Рассуждая далее, находим, что В это 2, а D это 6. В ответ запишем сумму дорог АС + DG = 30 + 8 = 38. 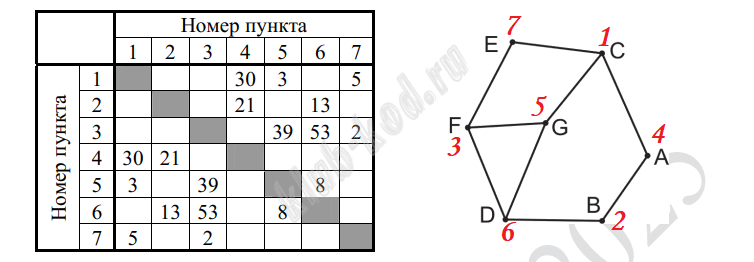 Ответ: 38 |
|||||||||||||||||||||
|
Задание 2. Построение таблиц истинности логических выражений Миша заполнял таблицу истинности логической функции ((w → y) → x) V ¬z но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx. |
Решение и ответ
ИЛИ print ('x y w z') получим таблицу: x y w z первый столбец z (все 1), последний х (все значения 0) Ответ: ZYWX |
|||||||||||||||||||||
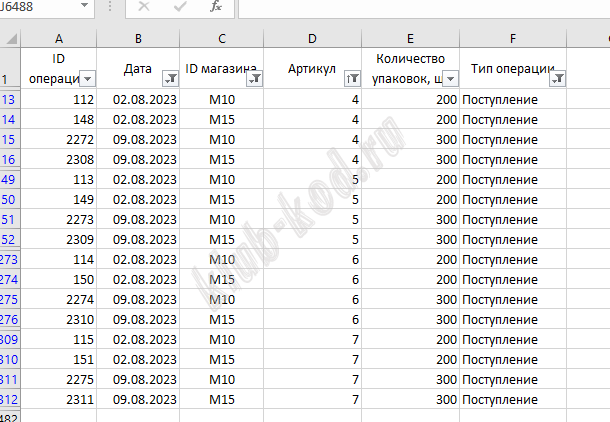
Задание 3. Базы данных. Файловая система В файле приведён фрагмент базы данных «Кондитерские изделия» о поставках конфет и печенья в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой половины июня 2023 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. внесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
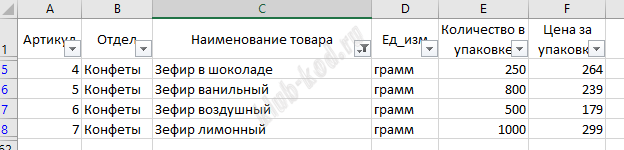
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
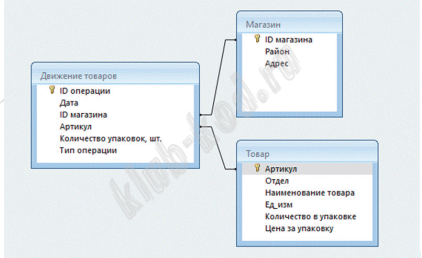
Используя информацию из приведённой базы данных, определите общую массу (в кг) всех видов зефира, полученных магазинами, расположенными на проспекте Революции, за период со 2 по 10 августа включительно. В ответе запишите только число. |
Решение и ответ На 3 листе применив фильтры, найдем ID магазинов.
Затем на 2 листе узнаем каким артикулам соответствуют разные вида зефира и какой вес упаковок На листе движение товаров найдем количество упаковок зефира каждого вида, поступившего в продажу в магазинах М10 и М15 со 2 по 10 августа. Каждого вида зефира получилось по 1000 упаковок . 1000 * (0, 25 + 0, 8 + 0, 5 + 1) = 2550 кг Ответ: 2550 |
|||||||||||||||||||||
|
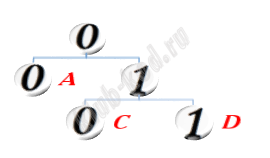
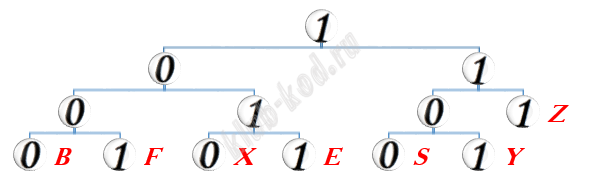
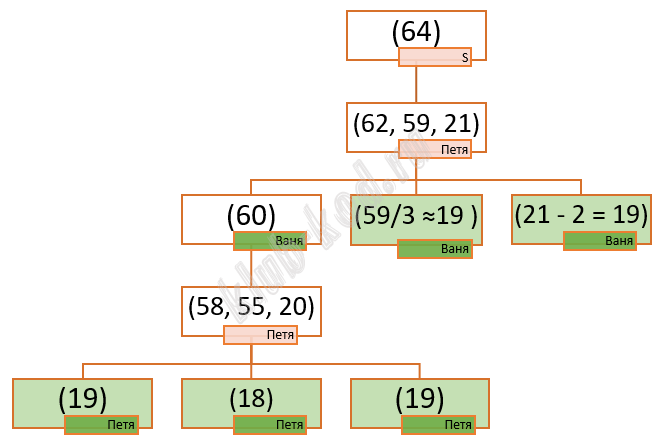
Задание 4. Кодирование и декодирование информации По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, B, C, D, E, F, S, X, Y, Z; для передачи используется неравномерный двоичный код. Для кодирования букв используются кодовые слова.
Укажите кратчайшее кодовое слово для буквы B, при котором код удовлетворяет условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением. |
Решение и ответ Построив дерево вариантов, получим свободную позицию для буквы В, это 1000.
Ответ: 1000 |
|||||||||||||||||||||
|
Задание 5. Анализ и построение алгоритмов для исполнителей На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. |
Решение и ответ Переведем алгоритм на язык программирования for N in range(12): #перебираем по порядку N
В полученных значениях N и R находим нужную строку, это число 109. Ответ: 109 |
|||||||||||||||||||||
|
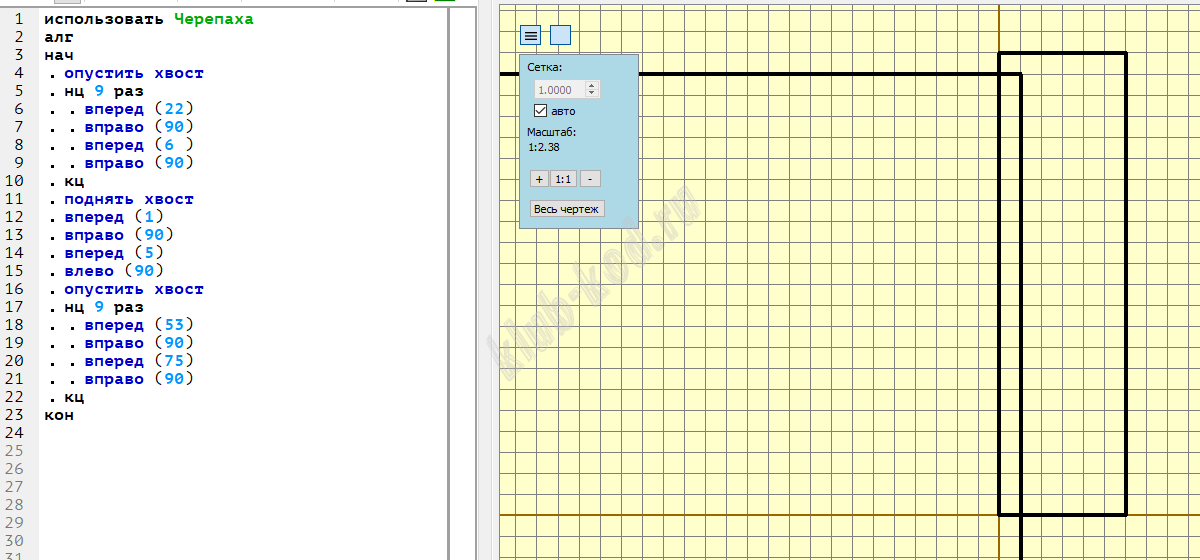
Задание 6. Анализ программ Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 6 команд: Черепахе был дан для исполнения следующий алгоритм: Определите периметр области пересечения фигур, ограниченных заданными алгоритмом линиями. |
Решение и ответ Сначала построим в Кумире фигуру:
Получилась фигура, состоящая из двух пересекающихся прямоугольников. Ответ: 44 |
|||||||||||||||||||||
|
Задание 7. Кодирование и декодирование информации. Передача информации Прибор автоматической фиксации нарушений правил дорожного движения делает цветные фотографии размером 1024×768 пикселей, используя палитру из 4096 цветов. Снимки сохраняются в памяти камеры, группируются в пакеты по несколько штук, а затем передаются в центр обработки информации со скоростью передачи данных 1 310 720 бит/с. В ответе запишите целое число.
|
Решение и ответ 1) Найдем размер одной фотографии
N = 2 i N = 4096 = 212 ⇒i = 12 бит
К = 1024 · 768 = 768 · 210 = 3 · 256 · 210 = 3 · 218 пикселей I1 =3 · 218 ·12 = 36 · 218 = 9 · 220 бит - вес одной фотографии 2)Найдем максимальный вес пакета I = v · t Iпакета = 1310720 · 300 = 393216000 бит = 160 · 213 · 300 = 16 · 213 · 3 · 8 · 125 = 375 · 220 бит 3) Найдем максимальное количество фотографий в пакете k = I пакета / I1 k = (375 · 220)/(9 · 220) = 41,(6) Ответ: 41 |
|||||||||||||||||||||
|
Задание 8. Перебор слов и системы счисления Определите количество 12-ричных пятизначных чисел, в записи которых ровно одна цифра 7 и не более трёх цифр с числовым значением, превышающим 8. |
Решение и ответ alf = '0123456789AB' print(k) Ответ: 67476 |
|||||||||||||||||||||
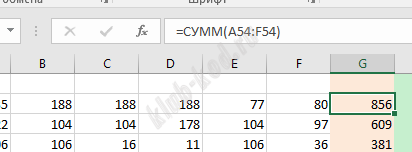
Задание 9. Работа с таблицами Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: В ответе запишите только число |
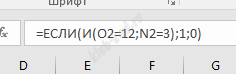
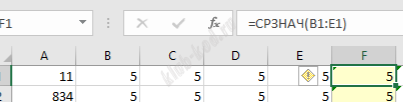
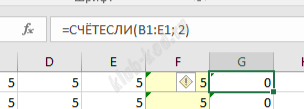
Решение и ответ При помощи формулы СЧЕТЕСЛИ посчитаем в следующих вспомогательных 6 столбцах сколько раз встречается каждое из чисел.
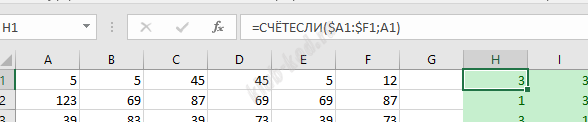 Далее в столбце N найдем количество троек.
Далее в столбце O найдем сумму значений в столбцах H:M. Сумма должна равняться 12, чтобы соблюдалось условие. Проверим соблюдение первого условия в столбце W. Таблица большая, поэтому дальше работаем с фильтром, выключим нули.
В столбце G найдем сумму чисел в столбцах A..F
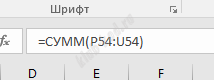
Добавим столбцы для проверки 2 условия. В столбцах P..U выведем повторяющиеся числа. Сумму этих значений поместим в столбец V.
Добавим второе условие к формуле в столбце W. Сумма значений столбца W будет ответом на задачу. Ответ: 273 |
|||||||||||||||||||||
Задание 10. Поиск символов в текстовом редакторе C помощью текстового редактора определите, сколько раз встречается сочетание букв «по» или «По» в составе других слов, включая сложные слова, соединённые дефисом, но не как отдельное слово в тексте глав XII и XIV третьей части тома 2 романа Л.Н. Толстого «Война и мир». В ответе |
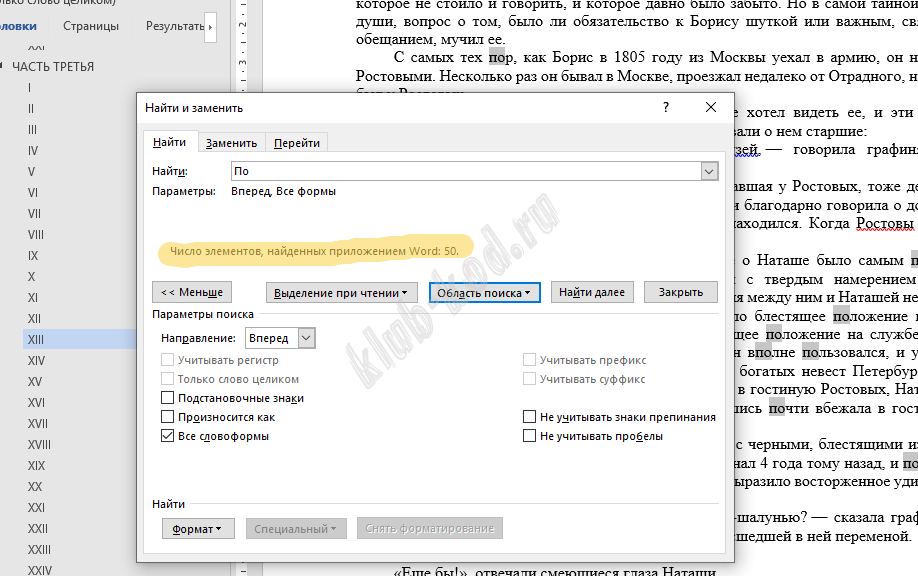
Решение и ответ В текстовом редакторе используем инструмент расширенный поиск. В строке поиска пишем по. Ставим галочку все словоформы. Потом выделяем 12 главу III части и указываем текущий фрагмент поиска. Получим 50. Далее ставим галочку слово целиком и снова выделяем 12 главу III части, указываем текущий фрагмент. Получим 3 соответствия. Значит в 12 главе ответом будет 50 - 3 = 47.
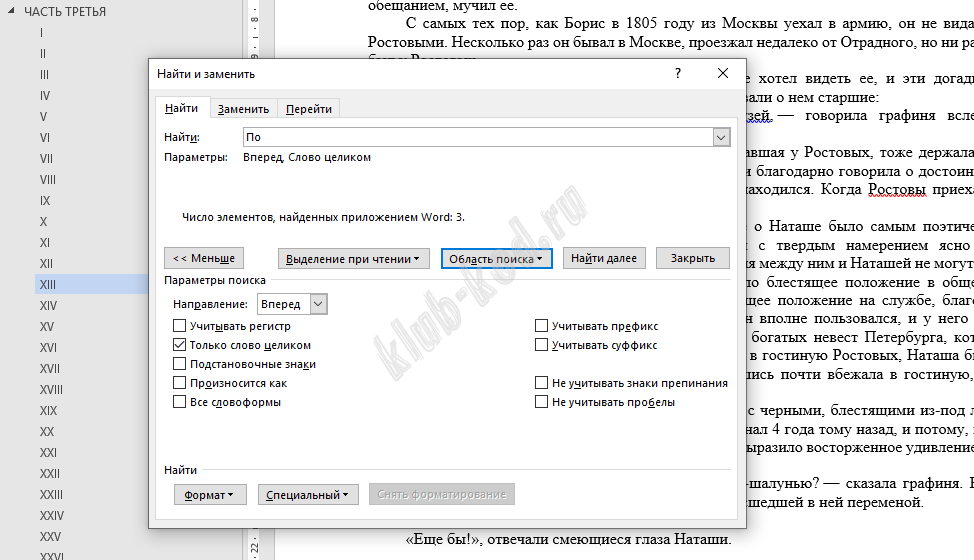
Проделаем те же действия в 14 главе III части, получим 62 - 7 = 55. Итого по двум главам, 47 + 55 = 103
Ответ: 103 |
|||||||||||||||||||||
|
Задание 11. Вычисление количества информации На предприятии каждой изготовленной детали присваивают серийный номер, содержащий десятичные цифры, 52 латинские буквы (с учётом регистра) и символы из 963-символьного специального алфавита. В базе данных для хранения каждого серийного номера отведено одинаковое и минимально возможное число байт. При этом используется посимвольное Известно, что для хранения 2000 серийных номеров отведено не более 693 Кбайт памяти. Определите максимально возможную длину серийного номера. В ответе запишите только целое число. |
Решение и ответ N: {десятичные цифры + 52 буквы + 963 символа специального алфавита} - всего 1025 символов N = 2 i, 1025 > 1024 ⇒ 2048 = 211, значит для кодирования одного символа нужно 11 бит I = K · i, ⇒ k = I/i I1=(693 · 210 ) / 2000 ≈ 354 байта округляем до целого числа байт k<=(354 · 8)/11 = 257,(45) округляем в меньшую сторону, чтобы поместились номера Ответ: 257 |
|||||||||||||||||||||
|
Задание 12. Выполнение алгоритмов для исполнителей Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить (v, w) Б) нашлось (v) Цикл В конструкции В конструкции Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 81 идущей подряд цифры 1? НАЧАЛО |
Решение и ответ s = 81 * '1' print (s) Ответ: 881 |
|||||||||||||||||||||
|
Задание 13. Организация компьютерных сетей. Адресация В терминологии сетей TCP/IP маской сети называют двоичное число, которое показывает, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу узла в этой сети. Адрес сети получается в результате применения поразрядной конъюнкции к заданному адресу узла и маске сети. Сеть задана IP-адресом 172.16.168.0 и маской сети 255.255.248.0. Сколько в этой сети IP-адресов, для которых количество единиц в двоичной записи IP-адреса не кратно 5? В ответе укажите только число |
Решение и ответ узел в сети: 172. 16. 168. 0 маска: 255. 255. 248. 0 адрес сети: 172. 16. 168. 0 Переведем в двоичный код 10101100. 00001000. 10101000. 00000000 - узел в сети В маске первые 21 единицы, значит последние 11 нулей соответствуют неизвестным узлам сети. Для этого воспользуемся формулой для вычисления количества перестановок с повторениями:
1) 0 единиц - 10101100. 00001000. 10101000. 00000000 -1 вариант Всего 1663 различных варианта Ответ: 1663 |
|||||||||||||||||||||
|
Задание 14. Кодирование чисел. Системы счисления Операнды арифметического выражения записаны в системе счисления с основанием 19. 98897x2119 + 2x92319 В записи чисел переменной x обозначена неизвестная цифра из алфавита 19-ричной системы счисления. Определите наибольшее значение x, при котором значение данного арифметического выражения кратно 18. Для найденного x вычислите частное от деления значения арифметического выражения на 18 и укажите его в ответе в десятичной системе счисления. Основание системы счисления указывать не нужно. ИЛИ Значение арифметического выражения 3 ∙ 31258 + 2 ∙ 6257 – 4 ∙ 6256 + 3 ∙ 1255 – 2 ∙ 254 – 2025 записали в системе счисления с основанием 25. Сколько значащих нулей содержится в этой записи? ИЛИ Значение арифметического выражения 7170 + 7100 – x, где x – целое положительное число, не превышающее 2030, записали в 7-ричной системе счисления. Определите наибольшее значение x, при котором в 7-ричной записи числа, являющегося значением данного арифметического выражения, содержится ровно 71 нуль. В ответе запишите число в десятичной системе счисления. |
Решение и ответ 1) for x in '0123456789abcdefghi': a = '98897' + x + '21' b = '2' + x + '923' c = int(a,19) + int(b, 19) if c % 18 == 0 : print(x, c // 18) 2) 3) if count == 71: Ответ: 469034148 или 10 или 2029 |
|||||||||||||||||||||
|
Задание 15. Преобразование логических выражений На числовой прямой даны два отрезка: P = [15; 40] и Q = [21; 63]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение (x ∈ P) → (((x ∈ Q) & ¬(x ∈ A)) → ¬(x ∈ P)) истинно (т.е. принимает значение 1) при любом значении переменной х. |
Решение и ответ P = range(15,41) for x in range (100): print (max(A) - min(A)) Ответ: 19 |
|||||||||||||||||||||
|
Задание 16. Рекурсивные алгоритмы Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = 1 при n = 1; F(n) = n × F(n - 1), если n > 1. Чему равно значение выражения (F(2024) + 2 * F(2023)) / F(2022)? |
Решение и ответ Значение данной функции проще и быстрее вычислить, выразив через F(2022) и сократив выражение:
(F(2024) + 2 * F(2023)) / F(2022) = (2024 * F(2023) + 2 * F(2023)) / (F(2022) = (F(2023) * 2026)/ (F(2022)= Ответ: 4 092 528 |
|||||||||||||||||||||
Задание 17. Проверка на делимость В файле содержится последовательность натуральных чисел. Её элементы могут принимать целые значения от 1 до 100 000 включительно. Определите количество пар последовательности, в которых остаток от деления хотя бы одного из элементов на 16 равен минимальному элементу последовательности. В ответе запишите количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче по |
Решение и ответ f = open('demo_2025_17.txt') p = [int(i) for i in f] f.close() M = 0 count = 0 M2 = 0 M = min(p) for i in range(len(p) -1): print(count, M2) Ответ: 1214 176024 |
|||||||||||||||||||||
Задание 18. Робот-сборщик монет Квадрат разлинован на N×N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. В «угловых» клетках поля – тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую нижнюю клетку поля. При разных запусках итоговые накопленные суммы могут различаться. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата. Пример входных данных:
|
Решение и ответ Ctrl+A Уменьшим ширину всех столбцов таблицы до 5. Скопируем таблицу рядом вместе со стенками и очистим ее клавишей Del.
Начинаем заполнение.
V1 = A1, W1=V1+B1 и протягиваем право, V2 =V1+A2 и протягиваем вниз,
W2 = МАКС(W1;V2)+B2 и протягиваем на всю таблицу копируя только значения, стенки не трогаем. Затем копируем формулы в верхней строке соответствующих ячеек и заполняем под стенами, копируем формулы в первом столбце соответствующих ячеек и заполняем ячейки правее стенок. 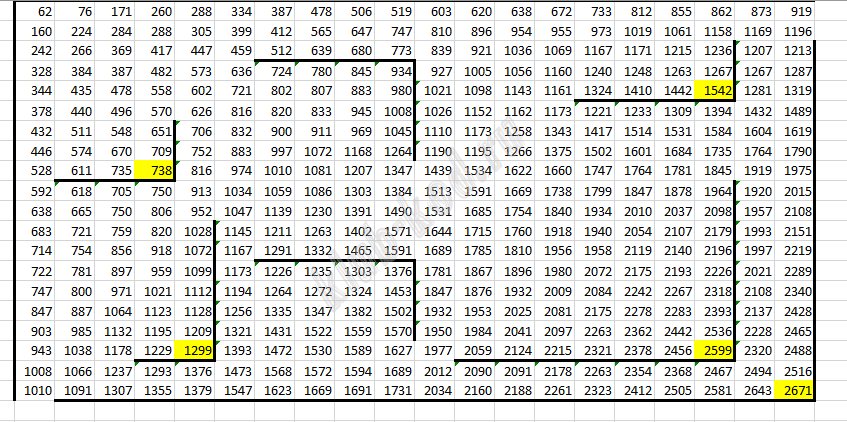 Находим максимальное значение из трех тупиковых клеток. Это 2671.
Далее Ctrl+H и заменяем МАКС на МИН. Получим:
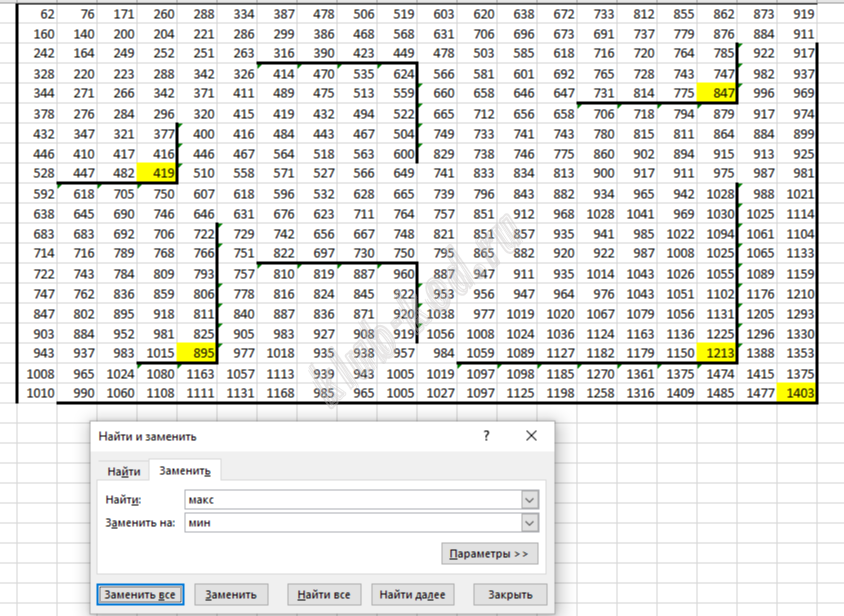 Ищем минимальное значение в тупиковых клетках. Это 419. Ответ: 2671 419 |
|||||||||||||||||||||
|
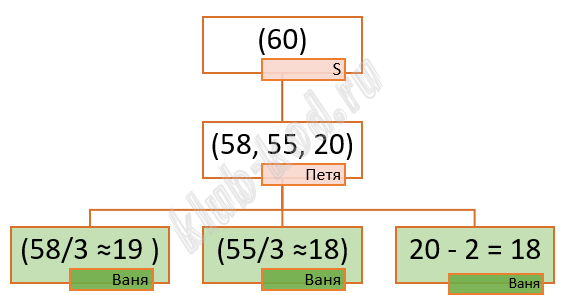
Задание 19. Выигрышная стратегия Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может: убрать из кучи два камня или убрать из кучи пять камней или уменьшить количество камней в куче в три раза (количество камней, полученное при делении, округляется до меньшего). Например, из кучи в 20 камней за один ход можно получить кучу из 18, 15 или 6 камней. |
Решение и ответ
Ответ: 60 |
|||||||||||||||||||||
|
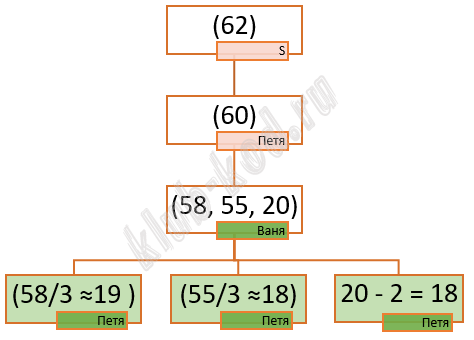
Задание 20. Выигрышная стратегия Для игры, описанной в задании 19, найдите два наименьших значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: Найденные значения запишите в ответе в порядке возрастания. |
Решение и ответ
Ответ: 62 63 |
|||||||||||||||||||||
|
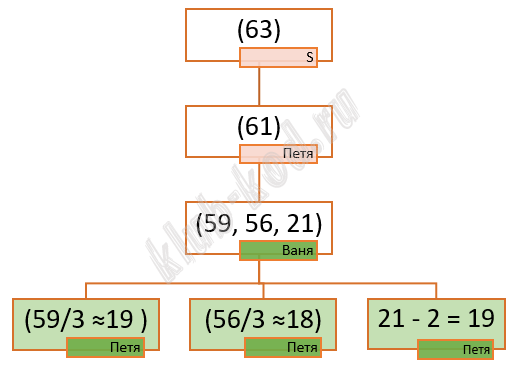
Задание 21. Выигрышная стратегия Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия: |
Решение и ответ
Ответ: 64 |
|||||||||||||||||||||
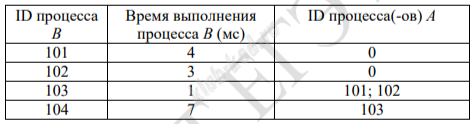
Задание 22. Анализ программы с циклами и условными операторами В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Приостановка выполнения процессов не допускается. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы – время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0. Типовой пример организации данных в файле:
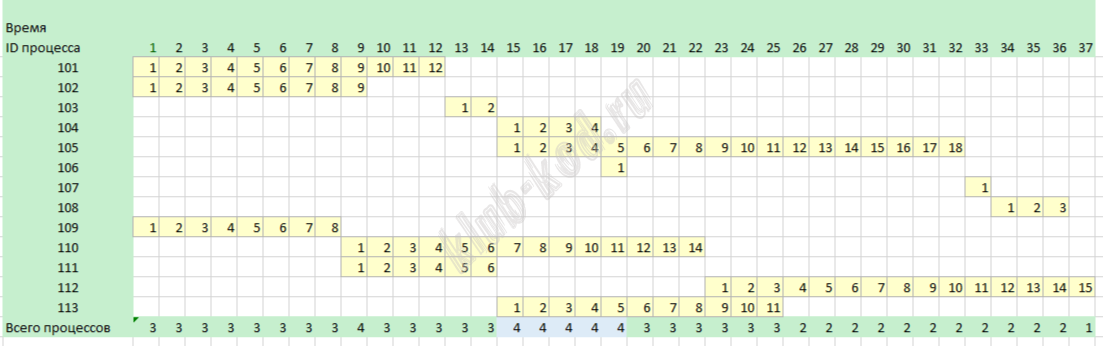
Определите максимальную продолжительность отрезка времени (в мс), в течение которого возможно одновременное выполнение максимального количества процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно и время окончания работы всех процессов минимально. Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемого файла. |
Решение и ответ |
|||||||||||||||||||||
|
Задание 23. Анализ программы с циклами и условными операторами Исполнитель преобразует число на экране. У исполнителя есть две команды, которые обозначены латинскими буквами: A. Вычти 2 Программа для исполнителя – это последовательность команд. Сколько существует программ, для которых при исходном числе 38 результатом является число 2 и при этом траектория вычислений содержит число 16? Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы ABB при исходном числе 13 траектория состоит из чисел 11, 5, 2 |
Решение и ответ def f(x, y): if x == y: return 1 if x < y: return 0 else: return f(x - 2, y) + f (x // 2, y) print (f(38, 16) * f(16, 2)) Ответ: 36 |
|||||||||||||||||||||
Задание 24. Анализ программы с циклами и условными операторами Текстовый файл состоит из цифр 0, 6, 7, 8, 9 и знаков арифметических операций «–» и «*» (вычитание и умножение). Определите максимальное количество символов в непрерывной последовательности, которая является корректным арифметическим выражением с целыми неотрицательными числами. В этом выражении никакие два знака арифметических операций не стоят рядом, в записи чисел отсутствуют незначащие (ведущие) нули и число 0 не имеет знака. В ответе укажите количество символов |
Решение и ответ f=open('demo_2025_24.txt') p= f.readline() f.close() M = 0 p = p.replace('**', ' ') p = p.replace('--', ' ') p = p.replace('-*', ' ') p = p.replace('*-', ' ') p = p.replace('-06', ' 6') p = p.replace('*06', ' 6') p = p.replace('-07', ' 7') p = p.replace('*07', ' 7') p = p.replace('-08', ' 8') p = p.replace('*08', ' 8') p = p.replace('-09', ' 9') p = p.replace('*09', ' 9') for i in p.split(): Ответ: 154 |
|||||||||||||||||||||
|
Задание 25. Анализ программы с циклами и условными операторами Пусть M – сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей у числа нет, то считаем значение M равным нулю. Напишите программу, которая перебирает целые числа, бо́льшие 800 000, в порядке возрастания и ищет среди них такие, для которых M оканчивается на 4. В ответе запишите в первом столбце таблицы первые пять найденных чисел в порядке возрастания, а во втором столбце – соответствующие им значения M. Например, для числа 20 М = 2 + 10 = 12. Количество строк в таблице для ответа избыточно ИЛИ Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы: Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске |
Решение и ответ 1) x = 800000 while count <5: if M % 10 ==4: 2) ИЛИ 351261495 183235 |
|||||||||||||||||||||
Задание 26. Анализ программы с циклами и условными операторами Во время сессии студенты сдают 4 экзамена, за каждый из которых можно получить от 2 до 5 баллов. Студенты, получившие хотя бы одну «двойку», считаются не сдавшими сессию. Результаты сессии публикуются в виде рейтингового списка, в котором сначала указаны идентификационные номера студентов (ID), сдавших сессию, в порядке убывания среднего балла за сессию, а в случае равенства средних баллов – в порядке возрастания ID. Затем располагаются ID студентов, не сдавших сессию: сначала – получивших одну «двойку», затем – две «двойки», потом ID студентов с тремя «двойками» и, наконец, ID студентов, получивших по 2 балла за каждый из экзаменов. Если студенты имеют одинаковое количество «двоек», то их ID в рейтинге располагаются в порядке возрастания. Повышенную стипендию получают студенты, занявшие в рейтинговом списке первые 25 % мест, при условии отсутствия у них «двоек». Гарантируется, что без «двоек» сессию сдали не менее 25 % студентов. Найдите ID студента, который занимает последнее место среди студентов с повышенной стипендией, а также ID первого в рейтинговом списке студента, который имеет более двух «двоек». В ответе запишите два целых положительных числа: сначала ID студента, который занимает последнее место среди студентов с повышенной стипендией, затем ID первого в рейтинговом списке студента, который имеет более двух «двоек». Входные данные В первой строке входного файла находится число N, обозначающее количество студентов (целое положительное число, не превышающее 10 000). Каждая из следующих N строк содержит 5 чисел через пробел: ID студента (целое положительное число, не превышающее 100 000) и четыре оценки, полученные им за сессию. Гарантируется, что общее число студентов N кратно 4 и хотя бы один студент имеет более двух «двоек». Во входном файле все ID различны. Выходные данные Два натуральных числа: искомые ID студентов в порядке, указанном в условии задачи. Типовой пример организации данных во входном файле
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов. |
Решение и ответ Откроем файл в excel с разделителями пробелами. Первое значение количество студентов можно удалить.
Далее считаем количество двоек у студентов
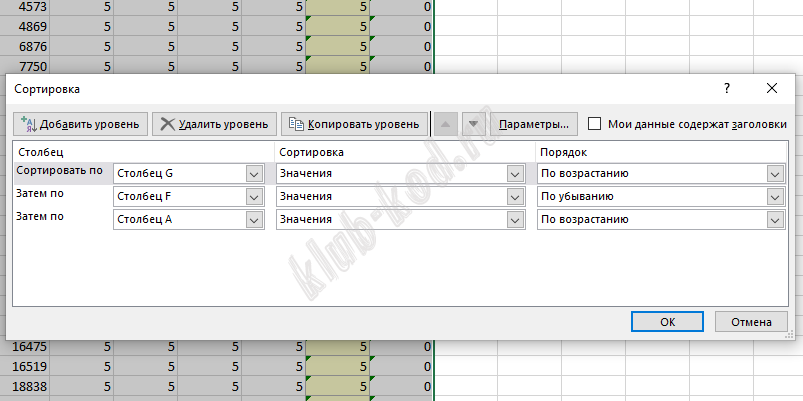
Далее применим многоуровневую сортировку
Осталось найти последнюю строку среди 25% лучших студентов. Это 0,25*9964 = 2491 строка. И ID студента 52326.
 И первую строку среди тех, кто получил более 2 двоек. Это студент с ID 635.  Ответ: 52326 635 |
|||||||||||||||||||||
Задание 27. Анализ программы с циклами и условными операторами Файлы txt Файлы xls Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике, лежащий внутри прямоугольника высотой H и шириной W. Каждая звезда обязательно принадлежит только одному из кластеров. Истинный центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Под расстоянием понимается расстояние Евклида между двумя точками A(x1, y1) и B(x2, y2) на плоскости, которое вычисляется по формуле:
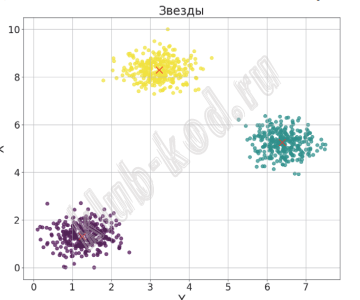
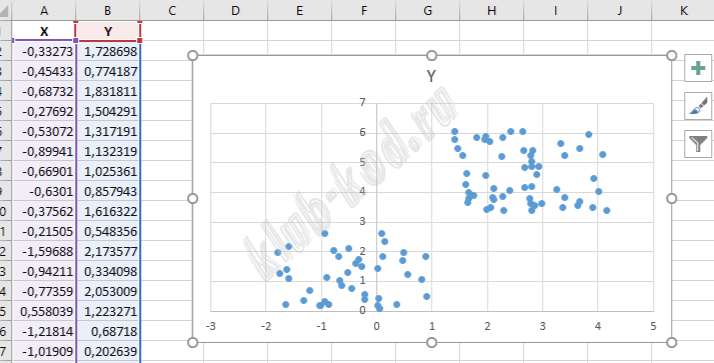
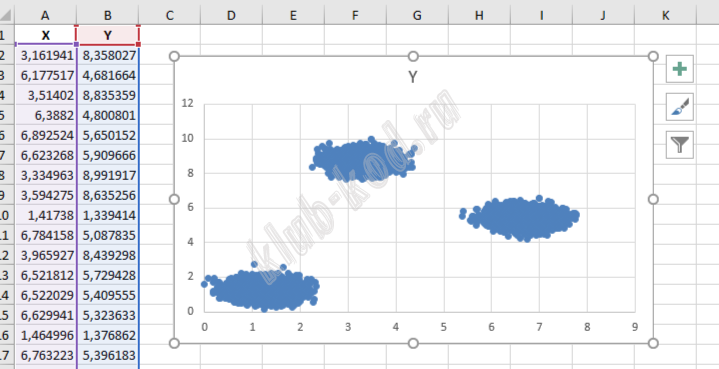
В файле A хранятся данные о звёздах двух кластеров, где H=3, W=3 для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y. Значения даны в условных единицах. Известно, что количество звёзд не превышает 1000. В файле Б хранятся данные о звёздах трёх кластеров, где H=3, W=3 для каждого кластера. Известно, что количество звёзд не превышает 10 000. Структура хранения информации о звездах в файле Б аналогична файлу А. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: Px – среднее арифметическое абсцисс центров кластеров, и Py – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения Px × 10 000 , затем целую часть произведения Py × 10 000 для файла А, во второй строке – аналогичные данные для файла Б. Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла. |
Решение и ответ В электронных таблицах по данным координатам построим точечные диаграммы, получим наглядное представление о кластерах.
По первой диаграмме видим два кластера:
1)(-2; 0) - (1;3)
2)(1; 3) - (5; 7)
Далее в текстовом файле уберем первую строку с заголовком и с помощью функции найти и заменить, изменим разделители запятые на точки.
def get_centr(box): #функция поиска центроиды – алгоритм полного перебора
m, x, y = 10 ** 20, 0, 0
for i in range(len(box)):
s = 0
for j in range(len(box)):
s += ((box[i][0] - box[j][0]) ** 2 + (box[i][1] - box[j][1]) ** 2) ** 0.5
if s < m:
m, x, y = s, box[i][0], box[i][1]
return (x, y)
f = open('demo_2025_27_A.txt')
k1, k2 = [], [] # создаем пустые массивы для трех кластеров
for i in f:
x, y = [float(e) for e in i.split()] # считываем координаты построчно
if -2 <= x <= 1 and 0 <= y <= 3:
k1.append((x, y)) #заполняем массив первого кластера
if 1 <= x <= 5 and 3 <= y <= 7:
k2.append((x, y)) #заполняем массив второго кластера
x1, y1 = get_centr(k1)
x2, y2 = get_centr(k2)
print(int((x1 + x2 ) / 2 * 10000), int((y1 + y2 ) / 2 * 10000))
По второй диаграмме видим три кластера: Далее в текстовом файле уберем первую строку с заголовком и с помощью функции найти и заменить, изменим разделители запятые на точки.
def get_centr(box): #функция поиска центроиды – алгоритм полного перебора
m, x, y = 10 ** 20, 0, 0
for i in range(len(box)):
s = 0
for j in range(len(box)):
s += ((box[i][0] - box[j][0]) ** 2 + (box[i][1] - box[j][1]) ** 2) ** 0.5
if s < m:
m, x, y = s, box[i][0], box[i][1]
return (x, y)
f = open('demo_2025_27_B.txt')
k1, k2, k3 = [], [], [] # создаем пустые массивы для трех кластеров
for i in f:
x, y = [float(e) for e in i.split()] # считываем координаты построчно
if 0 <= x <= 3 and 0 <= y <= 3:
k1.append((x, y)) #заполняем массив первого кластера
if 2 <= x <= 5 and 7 <= y <= 11:
k2.append((x, y)) #заполняем массив второго кластера
if 5 <= x <= 8 and 4 <= y <= 7:
k3.append((x, y)) #заполняем массив третьего кластера
x1, y1 = get_centr(k1)
x2, y2 = get_centr(k2)
x3, y3 = get_centr(k3)
print(int((x1 + x2 + x3) / 3 * 10000), int((y1 + y2 + y3) / 3 * 10000))
Ответ: 10738 30730 37522 51277 |
- Разбор демо-версий
- Просмотров: 38279