Разбор досрочного апрельского варианта 2024 по информатике

: Разбор демо-версий; 26 апреля 2024; Просмотров: 2011

Разбор досрочного апрельского варианта 2024 по информатике

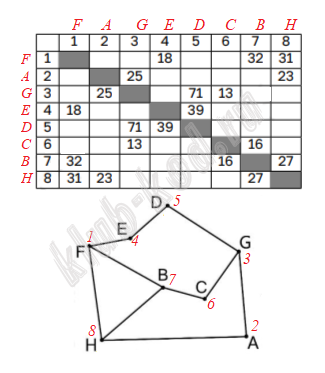
Задание 1. Анализ информационных моделей

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.

Определите, какова сумма протяжённостей дорог из пункта D в пункт E и из пункта D в пункт G.

Решение и ответ

Анализируя таблицу и граф, мы видим, что вершина G уникальна тем, что соединена с тремя вершинами. При этом вершина под номером 5 соединена с другой вершиной под номером 4, у которой тоже вес 2. Значит пятая вершина это D, а четвертая вершина это Е, а 1-ая вершина это F. Далее видим что первая соединена с 7 и 8. 7-я с 6-ой, 6-я с 3-ей. Значит В это 7, С это 6. Следовательно Н это 8, а вершина А это 2.

Ответом будет DE + DG = 71 + 39 = 110

Ответ: 110

Задание 2. Построение таблиц истинности логических выражений

Логическая функция F задаётся выражением:
(y ≡ ¬x) → ((z ∨ x) ≡ y)

Ниже представлен фрагмент таблицы истинности функции F содержащий неповторяющиеся строки, при которых функция F ложна.

???	???	???	F
1	1		0
0		0	0
0	0		0

Определите, какому столбцу истинности функции соответствует каждая переменная x, y, z.

Решение и ответ

print('x y z')
for x in range (2):
for y in range(2):
for z in range(2):
f = (y == (not(x))) <= ((z or x) == y)
if not f:
print (x, y, z)

получим таблицу:

x y z
0 1 0
1 0 0
1 0 1

и определим, что единственное решение, это - ZXY

Ответ: ZXY

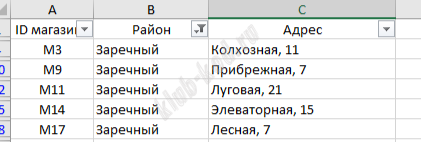
Задание выполняется с использованием прилагаемых файлов.
Файл с данными

Задание 3. Базы данных. Файловая система

В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины
районов города. База данных состоит из трёх таблиц.

Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение января 2024 г., а также информацию о проданных товарах. Поле «Тип операции» содержит значение «Поступление» или «Продажа», а в соответствующее поле «Количество упаковок, шт.» занесена информация о том, сколько упаковок товара поступило в
магазин или было продано в течение дня.
Заголовок таблицы имеет следующий вид.

Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.

Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.

На рисунке приведена схема указанной базы данных

Используя информацию из приведённой базы данных, определите на сколько изменилось количество килограмм имбирных пряников в магазинах района Заречный за период с 3 по 10 июня включительно.

Решение и ответ

На 3 листе применив фильтры, найдем ID магазинов.

Затем на 2 листе узнаем какому артикулу соответствуют имбирные пряники и какой вес упаковок

На листе движение товаров найдем количество упаковок имбирных пряников ,поступивших в продажу с 3 по 10 июня включительно.

Получим, что поступило в магазины Заречного района в этот период 38800 упаковок имбирных пряников по 0, 5 кг, то есть 19 400 кг.
Продали 30660 упаковок, то есть 15 330 кг.

19 400 - 15 330 = 4 070 кг

Ответ: 4070

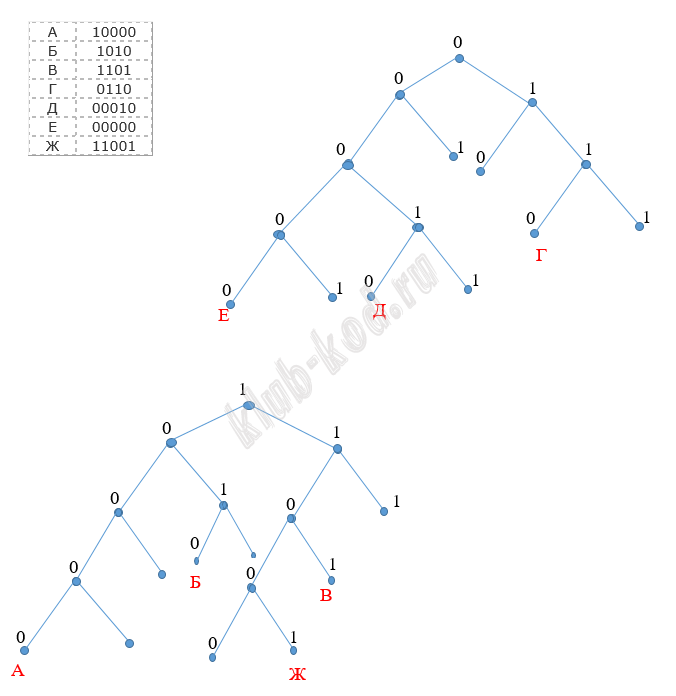
Задание 4. Кодирование и декодирование информации

По каналу связи передаются цифровые сообщения, содержащие только восемь букв: А, Б, В, Г, Д, Е, Ж и З. Кодовые слова для некоторых букв известны. Так, буквам А, Б, В, Г, Д, Е, Ж соответствуют кодовые слова 10000, 1010, 1101, 0110, 00010, 00000, 11001 соответственно.

Укажите кратчайшее кодовое слово для буквы З, при котором гарантируется однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение и ответ

Построив дерево вариантов, получим три свободные позиций с наименьшим числовым значением. Это 001, 010 и 111. Код с наименьшим значением это 001.

Ответ: 001

Задание 5. Анализ и построение алгоритмов для исполнителей

Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам:

1. Складываются первая и третья, а также вторая и четвёртая цифры.
2. Полученные два числа записываются друг за другом в порядке убывания без разделителей.

Пример. Исходное число: 1234. Сумма: 1 + 3 = 4; 2 + 4 = 6. Результат: 64.
Укажите наибольшее число, при обработке которого автомат выдаёт результат 113.

Решение и ответ

for x in range (9999, 999, -1):
s = str(x)
x1 = int(s[0]) + int(s[2])
x2 = int(s[1]) + int(s[3])
if x1 > x2:
y = str(x1) + str(x2)
else:
y = str(x2) + str(x1)
if y == '113':
print(x)
break

Ответ: 9320

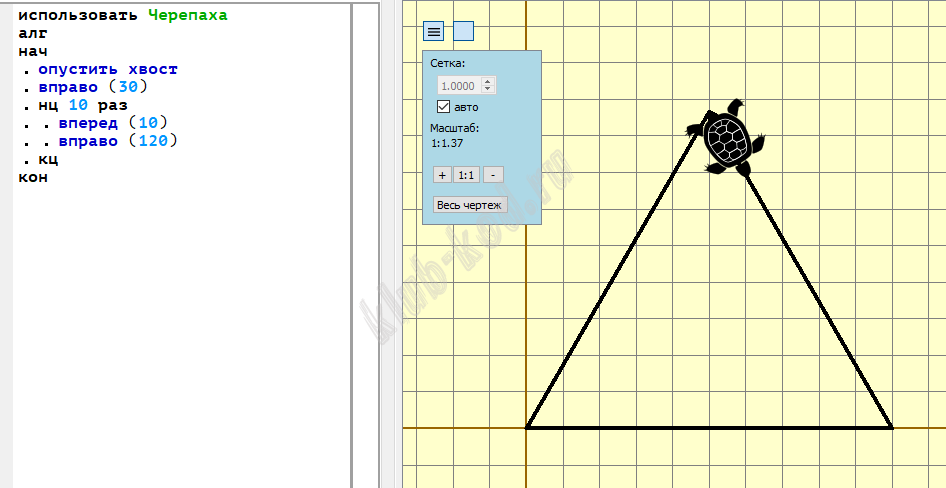
Задание 6. Анализ программ

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения.

У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори k [Команда1 Команда2 …КомандаS] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:
Направо 30 Повтори 10 [Вперёд 10 Направо 120].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

Решение и ответ

Сначала построим в Кумире фигуру:

count = 0
k = 3**0.5

for x in range(1,20):
for y in range(1,20):
if y < k * x and y < -k * x + 10 * k:
count +=1

print (count)

Ответ: 38

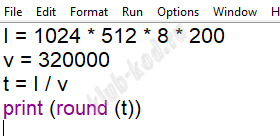
Задание 7. Кодирование и декодирование информации. Передача информации

Прибор автоматической фиксации нарушений правил дорожного движения делает цветные фотографии размером 1024 на 512 пикселей, используя палитру из 256 цветов. Снимки сохраняются в памяти камеры, группируются в пакеты по 200 шт., затем передаются в центр обработки информации со скоростью передачи данных 320 000 бит/с.

Сколько секунд требуется для передачи одного полного пакета фотографий?

В ответе запишите только целую часть полученного числа.

Решение и ответ

Ответ: 2621

Задание 8. Перебор слов и системы счисления

Сколько существует четверичных пятизначных чисел, в которых цифра 0 не стоит рядом с цифрой 2, и цифра 1 не стоит рядом с цифрой 3?

Решение и ответ

* * * * * - пятизначное число, алфавит: {0, 1, 2, 3}

alf = '0123'
count = 0

for x1 in alf[1:]:
for x2 in alf:
for x3 in alf:
for x4 in alf:
for x4 in alf:
x = x1 + x2 + x3 + x4 + x5
if x.count ('02') == 0 and x.count ('20') == 0 and x.count ('13') == 0 and x.count ('31') == 0:
count +=1

print (count)

Ответ: 243

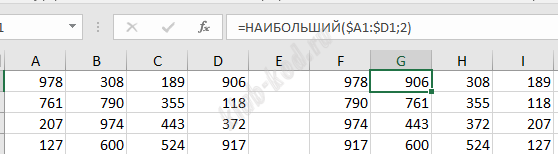
Задание выполняется с использованием прилагаемых файлов
Файл с данными

Задание 9. Работа с таблицами

Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа.

Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
— максимальное число строки меньше суммы трёх оставшихся чисел;
— четыре числа строки можно разбить на две пары чисел с равными суммами.

В ответе запишите только число.

Решение и ответ

При помощи формулы НАИБОЛЬШИЙ упорядочим все четыре числа.

Далее найдем проверим первое условие, чтобы максимальный элемент был меньше суммы остальных.

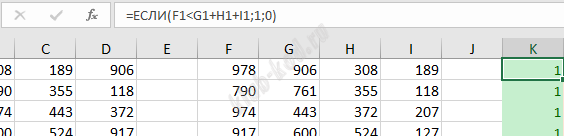
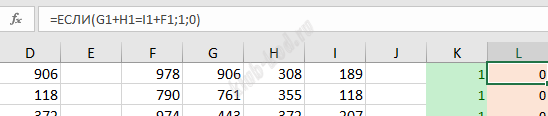
Далее проверим второе условие, наличие равных сумм пар элементов. Это возможно если сложить меньшее с большим, а средние между собой.

Проверим выполнение двух условий одновременно.

Сумма значений столбца М будет ответом на задачу.

Ответ: 10

Задание выполняется с использованием прилагаемых файлов
Файл с данными

Задание 10. Поиск символов в текстовом редакторе

В файле приведен текст произведения «Поединок» А. Куприна. Определите, сколько раз встречается сочетание «по» или «По» только в составе других слов, но не как отдельное слово.

В ответе укажите только число.

Решение и ответ

В текстовом редакторе используем инструмент расширенный поиск. В строке поиска пишем По. Ставим галочку все словоформы и область поиска - основной документ. Получим 3905. Далее ставим галочку слово целиком. Получим 328 соответствий. Ответом будет 3905 - 328 = 3577.

Ответ: 3577

Задание 11. Вычисление количества информации

При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 11 символов и содержащий только символы А, Б, В, Г, Д. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).

Определите объём памяти в байтах, отводимый этой программой для записи 20 паролей.

Решение и ответ

Pass: {**....*} – всего 11 символов

N: {А, Б, В, Г, Д} - всего 5 символов

N = 2ⁱ, 5 > 4 ⇒ 8 = 2³, значит для кодирования одного символа нужно 3 бита

I = K · i, I = 11 · 3 = 33 бита ≈ 5 байт – отводится на 1 пароль

I₂₀ = 20 · 5 = 100 байт – всего.

Ответ: 100

Задание 12. Выполнение алгоритмов для исполнителей

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.

Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (8888)
заменить (8888, 44)
заменить (4444, 848)
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой выше программе поступает строка, содержащая n цифр «8» (3 < n < 1000). Определите наименьшее возможное количество цифр «8» в строке, при котором cумма цифр строки, получившейся в результате выполнения программы, равна не менее 52.

Решение и ответ

for n in range(3, 100001):
s = '8' * n
while '8888' in s:
s = s.replace ('8888', '44',1)
s = s.replace ('4444', '848',1)

sum_s = 0
for i in s:
sum_s += int(i)
if sum_s >= 52:
print(n)
break

Ответ: 18

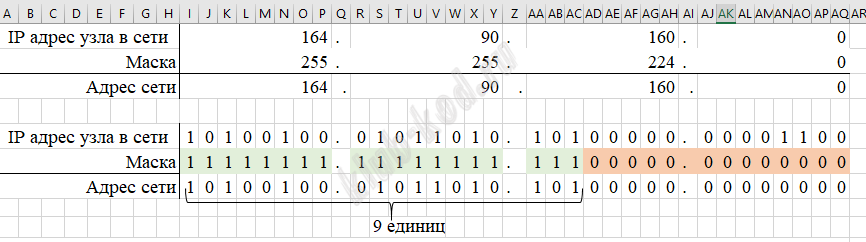
Задание 13. Организация компьютерных сетей. Адресация

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места – нули. Обычно маска записывается по тем же правилам, что и IP-адрес, – в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа.
Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

Сеть задана IP-адресом 164.90.160.0 и сетевой маской 255.255.224.0. Сколько в этой сети IP-адресов, для которых количество единиц в двоичной записи IP-адреса кратно 4?

В ответе укажите только число.

Решение и ответ

В адресе сети получается 9 единиц. В данной сети всего 8192 адреса, 213 = 8192. То есть 13 мест для перестановок с повторениями из 0 и 1. Значит для того, чтобы количество единиц было кратно 4, их в IP адресе узла должно быть 12, 16 или 20. Воспользуемся формулой:

где n = n1 + n2 +... + nk, n1 - перестановки единиц, n2 - перестановки нулей

1) х = 3 ⇒ P = 13! / (3! ⋅ 10!) = 286

2) x = 7 ⇒ P = 13! / (7! ⋅ 6!) = 1716

3) х = 11 ⇒ P = 13! / (11! ⋅ 2!) = 78

Итого, 286 + 1716 + 78 = 2080

Ответ: 2080

Задание 14. Кодирование чисел. Системы счисления

Операнды арифметического выражения записаны в системе счисления с основанием 27:

123x24₂₇+ x178₂₇

В записи чисел переменной обозначена неизвестная цифра из алфавита 27-ричной системы счисления. Определите наибольшее значение, при котором значение данного арифметического выражения кратно 26. Для найденного значения вычислите частное от деления значения арифметического выражения на 26 и укажите его в ответе в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение и ответ

for x in range (26, 0, -1):
a = 1* 27**5 + 2 * 27**4 + 3 * 27**3 + x* 27**2 + 2 * 27**1 + 4
b = x * 27**3 + 1 * 27**2 + 7*27**1 + 8
c = a + b
if c % 26 == 0 :
print(c // 26)
break

Ответ: 614697

Задание 15. Преобразование логических выражений

На числовой прямой даны два отрезка: P = [8; 47] и Q = [5; 18].
Укажите наименьшую возможную длину такого отрезка A, что формула

((x ∉ A) → (x ∉ P)) ∨ (x ∈ Q)

тождественно истинна при любых значениях переменной x

Решение и ответ

P = range(8,48)
Q = range(5,19)
A = []

for x in range (100):
f = ((x not in A) <= (x not in P)) or (x in Q)
if not f:
A.append(x)
print (max(A) - min(A))

Ответ: 28

Задание 16. Рекурсивные алгоритмы

Алгоритм вычисления значений функции F(n), где n - целое неотрицательное, задан следующими соотношениями:
F(1) = 1
F(2) = 2
F(n) = n + F(n - 1)
Чему равно значение выражения F(2024) - F(2023)?

Решение и ответ

F(2024) - F(2023) = 2024 + F(2023) - F(2023) = 2024

Ответ: 2024

Задание выполняется с использованием прилагаемых файлов
Файл с данными

Задание 17. Проверка на делимость

В файле содержится последовательность целых чисел, не превышающих по модулю 10 000. Определите количество троек элементов последовательности, в которых хотя бы один элемент тройки — трёхзначное число, сумма всех элементов этой тройки не больше, чем максимальный элемент из этой тройки, и максимальный элемент тройки не оканчивается на цифру 1.

В ответе запишите два числа: сначала количество найденных троек,
затем минимальную сумму элементов таких троек.

В данной задаче под тройкой подразумевается три идущих подряд элемента последовательности.

Решение и ответ

f = open('17_3.txt')
p = [int(i) for i in f]
f.close()
count = 0
m3 = float ('inf')

for i in range(len(p) -2):
s = p[i] + p[i+1] + p[i+2]
m = max(p[i], p[i+1], p[i+2])
if ((100 <= abs(p[i])< 1000) or (100 <= abs(p[i + 1]) < 1000) or (100 <= abs(p[i + 2]) < 1000)) and (s <= m) and (str(m)[-1] != '1'):
count += 1
m3 = min(m3, s)

print(count, m3)

Ответ: 1677 -20077

Задание выполняется с использованием прилагаемых файлов
Файл с данными

Задание 18. Робот-сборщик монет

Квадрат разлинован на N×N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку; по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.

В «угловых» клетках поля — тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую нижнюю клетку поля.
При разных запусках итоговые накопленные суммы могут различаться. Определите максимальную и минимальную денежные суммы, среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута.
Исходные данные записаны в файле в виде электронной таблице размером N × N, каждая ячейка которой соответствует клетке квадрата.

Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута. В ответе укажите два числа — сначала максимальную сумму, затем минимальную.

Решение и ответ

Ctrl+A Уменьшим ширину всех столбцов таблицы до 5. Скопируем таблицу рядом вместе со стенками и очистим ее клавишей Del.

Начинаем заполнение.

АА1 = A1, АВ1=АА1+B1 и протягиваем право, АА2 =АА1+A2 и протягиваем вниз,
АВ2 = МАКС(АВ1;АА2)+B2 и протягиваем на всю таблицу копируя только значения, стенки не трогаем. Затем копируем формулы в верхней строке соответствующих ячеек и заполняем под стенами, копируем формулы в первом столбце соответствующих ячеек и заполняем ячейки правее стенок.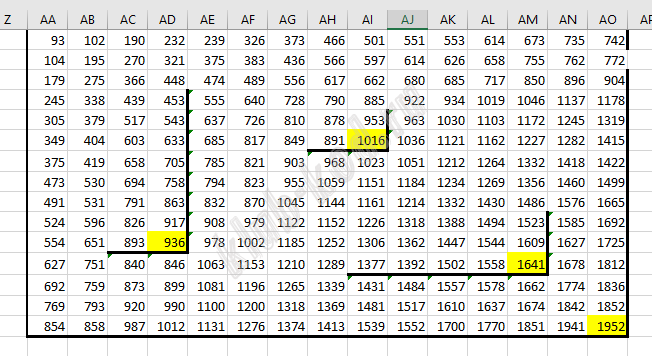

Находим максимальное значение из трех тупиковых клеток. Это 1952.

Далее Ctrl+H и заменяем МАКС на МИН. Получим:

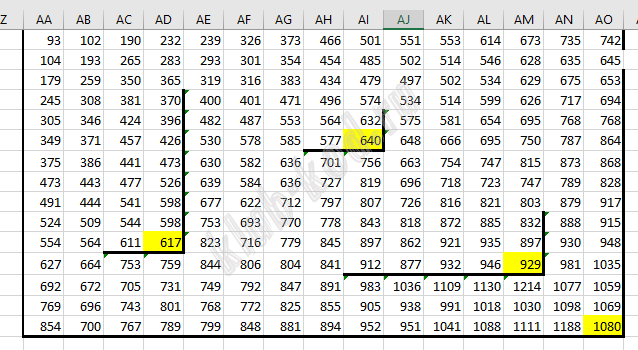Ищем минимальное значение в тупиковых клетках. Это 1080.

Ответ: 1952 617

Задание 19. Выигрышная стратегия

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч два камня или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 74.

Победителем считается игрок, сделавший последний ход, т.е. первым получивший позицию, в которой в кучах будет 74 или больше камней.

В начальный момент в первой куче было 7 камней, во второй куче – S камней, 1 ≤ S ≤ 66.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.

Решение и ответ

from functools import lru_cache
def tree(z):
x, y = z
return (x+2, y), (x, y+2), (x*2, y), (x, y*2)

@lru_cache(None)

def g(z):
if sum(z) >= 74: return 'END'
if any(g(i) == 'END' for i in tree(z)):
return 'p1'
if any(g(i) == 'p1' for i in tree(z)):
return 'v1'

for s in range(1, 67):
if g((7,s)) == 'v1':
print(s)

Ответ: 17

Задание 20. Выигрышная стратегия

Для игры, описанной в задании 19, найдите такое минимальное значения S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
– Петя не может выиграть за один ход;
– Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Решение и ответ

from functools import lru_cache
def tree(z):

x, y = z

return (x+2, y), (x, y+2), (x*2, y), (x, y*2)

@lru_cache(None)

def g(z):

if sum(z) >= 74: return 'END'

if any(g(i) == 'END' for i in tree(z)):

return 'p1'

if all(g(i) == 'p1' for i in tree(z)):

return 'v1'

if any(g(i) == 'v1' for i in tree(z)):

return 'p2'

for s in range(1, 67):

if g((7,s)) == 'p2':

print(s)

break

Ответ: 29

Задание 21. Выигрышная стратегия

Для игры, описанной в задании 19, найдите два минимальных значение S, при которых одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Найденные значения запишите в ответе в порядке возрастания.

Решение и ответ

from functools import lru_cache

def tree(z):

x, y = z

return (x+2, y), (x, y+2), (x*2, y), (x, y*2)

@lru_cache(None)

def g(z):

if sum(z) >= 74: return 'END'

if any(g(i) == 'END' for i in tree(z)):

return 'p1'

if all(g(i) == 'p1' for i in tree(z)):

return 'v1'

if any(g(i) == 'v1' for i in tree(z)):

return 'p2'

if all(g(i) == 'p2' or g(i) == 'p1' for i in tree(z)):

return 'v2'

for s in range(1, 67):

if g((7,s)) == 'v2':

print(s)

Ответ: 27 30

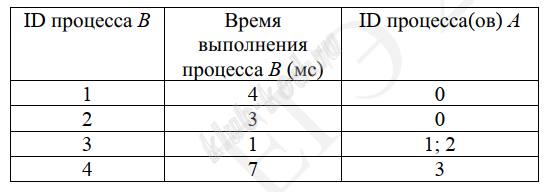
Задание выполняется с использованием прилагаемых файлов
Файл с данными

Задание 22. Анализ программы с циклами и условными операторами

В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно.
Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы A и B могут выполняться только последовательно.

Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс независимый, то в таблице указано значение 0.

Типовой пример организации данных в файле:

Определите максимальную длительность отрезка времени (в мс), в течение которого возможно одновременное выполнение двух процессов.

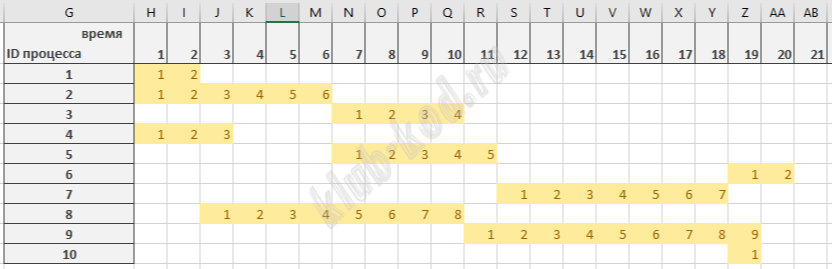
Решение и ответ

В данной задаче нужно найти максимальное время выполнения 2-х параллельных процессов. Для этого построим таблицу, в которой наглядно видно выполнение всех процессов.

Если подвинуть процессы 4 и 5 и от них зависящие, получим 23 мс - максимальное время выполнения 2-х процессов.

Ответ: 23

Задание 23. Анализ программы с циклами и условными операторами

У исполнителя Калькулятор имеются две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Программа для исполнителя – это последовательность команд.
Сколько существует программ, для которых при исходном числе 3 результатом является число 17, и при этом траектория вычислений содержит числа 7 и 10?

Решение и ответ

def f(x,y):
if x == y:
return 1
elif x > y:
return 0
else:
return f(x + 1, y) + f(x * 2, y)

print (f(3,7)* f(7,10) * f(10, 17))

Ответ: 2

Задание выполняется с использованием прилагаемых файлов
Файл с данными

Задание 24. Анализ программы с циклами и условными операторами

Текстовый файл состоит не более чем из 10⁶ букв A, B, C, D. Найдите длину максимальной последовательности символов, которая не содержит подряд идущих букв A. Для выполнения этого задания следует написать программу. В ответе запишите значение данного выражения.

Решение и ответ

f = open('24.txt')
s = f.readline()
m = 0
s = s.replace('AA', 'A A')

for i in s.split():
m = max(len(i), m)
print(m)

Ответ: 184

Задание 25. Анализ программы с циклами и условными операторами

Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы:
— символ «?» означает ровно одну произвольную цифру;
— символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность.
Например, маске 123*4?5 соответствуют числа 123405 и 12300425.
Найдите все числа, меньшие 108, соответствующие маске 2*93?28 и делящиеся без остатка на 2024.

В качестве ответа приведите все найденные числа в порядке возрастания, справа от каждого числа выведите результат его деления на 2024.

Решение и ответ

from fnmatch import *
for i in range(2024, 10 ** 8 + 1, 2024):
if fnmatch(str(i), '2*93?28'):
print(i, i // 2024)

Ответ:
25293928 12497
29493728 14572

Задание выполняется с использованием прилагаемых файлов
Файл с данными

Задание 26. Анализ программы с циклами и условными операторами

В кондитерской имеется N различных слоев торта. Слои торта можно установить один на другой, если размер каждого слоя на 6 единиц меньше размера предыдущего. Определите наибольшее количество слоев, которое можно использовать для создания одного торта, и максимально возможный размер самого маленького слоя торта.
Входные данные представлены в файле следующим образом. В первой строке входного файла записано число N – количество слоев торта в кондитерской (натуральное число,
не превышающее 10 000). В каждой из следующих N строк находится значение размера
очередного слоя торта (натуральное число, не превышающее 10 000).
Запишите в ответе два целых числа: сначала наибольшее количество слоев, которое
можно использовать для создания одного торта, затем максимально возможный размер
самого маленького слоя торта в таком наборе.
Пример входного файла:
5
43
40
32
40
30
При таких исходных данных условию задачи удовлетворяют наборы слоев торта с размерами 30, 40 и 43 или 32, 40 и 43 соответственно. В обоих случаях количество слоев равно 3, а размер самого маленького слоя торта равен 32. Ответ: 3 32.

Решение и ответ

Откроем файл в excel с разделителями пробелами. Первое значение количество строк можно удалить. Далее отсортируем по убыванию первый столбец. После применяем формулы:

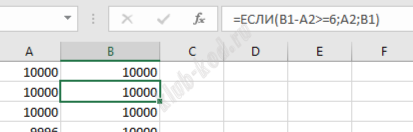Далее убираем дубли

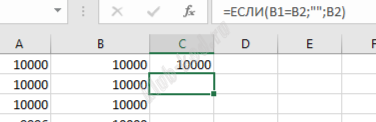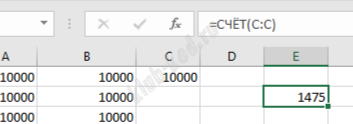Сумма значений в столбце С равна 1475. Далее найдем максимальный размер самого маленького слоя торта, он равен 6.

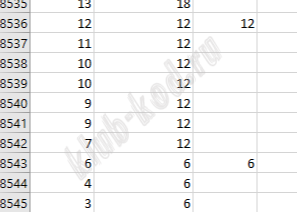Ответ: 1475 6

Задание выполняется с использованием прилагаемых файлов
Файл A
Файл B

Задание 27. Анализ программы с циклами и условными операторами

В городе расположена кольцевая автодорога длиной в N километров с движением в обе стороны. На автодороге расположено K пунктов приема мусора определенной вместимости. Нулевой километр и N-й километр находятся в одной точке. Для перевозки мусора используются мусоровозы вместимостью 15 единиц. Стоимость доставки мусора вычисляется как вместимость пункта сбора, умноженная на расстояние от пункта сбора мусора до мусороперерабатывающего завода. Определите минимальные расходы на доставку мусора со всех пунктов приёма мусора, если мусороперерабатывающий завод расположен на кольцевой автодороге на территории одного из пунктов приёма мусора.

Входные данные. Даны два входных файла (файл A и файл B), каждый содержит в первой строке натуральное число N и K – длина автодороги (1 ≤ N ≤ 10 000 000) и количество пунктов приёма мусора (1 ≤ K ≤ 10 000 000). В каждой из следующих K строк записано два целых числа: номер километра автодороги, на котором находится пункт приёма мусора, и количество мусора в каждом из пунктов (натуральное число, не превышающее 10 000).

Данные указаны в порядке расположения пунктов приёма мусора на автодороге.

Пример входного файла:
20 5
2 10
5 7
11 12
13 8
17 15

Для данного примера ответ — 80, если вместимость мусоровоза — 3 (минимальная стоимость доставки мусора, если мусоровоз стоит в пункте 17: 0 ⋅ 3 + 4 ⋅ 3 + 6 ⋅ 4 + 8 ⋅ 3 + 5 ⋅ 4 = 80).
В ответе укажите два числа: сначала искомое значение для файла A, затем для файла B.

Решение и ответ

Решение для файла А. Наименьшую стоимость получим, если разместим мусороперерабатывающий завод на 22 км
from math import ceil
f = open('27A.txt')
n, k = map(int, f.readline().split())
P = []
V = []

for i in range(k):
p, v = map(int, f.readline().split())
P.append(p)
V.append (ceil(v/15))

m = float('inf')
for i in range(k):
cost = 0
for j in range(k):
s = min(abs(P[i] - P[j]), n - abs(P[i] - P[j]))
cost += s * V[j]
print(i, cost)

m = min(cost, m)
print(m)

или

from math import ceil
f = open('27A.txt')
n, k = map(int, f.readline().split())
P = []
V = []
dp = []
p = 2

for i in range(k): # заполняем массивы
ps = p
p, v = map(int, f.readline().split()) #считываем построчно данные
V.append(ceil(v/15)) # заполняем массив с данными количества мусоровозов в каждом пункте
P.append (p) # массив содержащий пункты приемы мусора (км дороги)
dp.append (p - ps) # массив, содержащий расстояния между соседними пунктами

dp[0] = n - P[k-1] + P[0]
min_s = 10000

for i in range(k):# в этом цикле пункт двигаем в 0-ю позицию
dp. append (dp[0])# последний элемент закольцовываем
V.append(V[0])# последний элемент закольцовываем
s = 0
j = 1
dp[0] = dp[0] * 0

while sum(dp[:j+1]) <= n//2:# считаем сумму доставки для 1-ой половины дороги
s += sum(dp[:j+1]) * V[j]
j += 1

j = k - 1
while sum(dp[k : j : -1 ]) <= n//2:# считаем сумму доставки для 2-ой половины дороги
s += sum(dp[k : j :-1]) * V[j]
j -= 1

min_s = min(min_s, s)
del(V[0])
del(dp[0])

print(min_s)

Ответ: 921