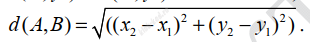|
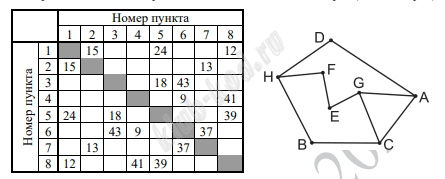
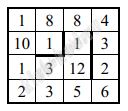
Задание 1. Анализ информационных моделей На рисунке изображена схема дорог N-ского района. В таблице звездочкой обозначено наличие дороги из одного населенного пункта в другой.
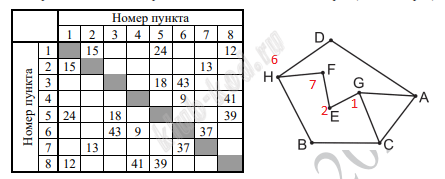
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта G в пункт E и из пункта F в пункт H. В ответе запишите целое число. |
Решение и ответ Анализируя таблицу и граф, расставим веса вершин. Это двойки и тройки. Найдем уникальную вершину. Это вершина H, которая соединена с тремя вершинами двойками, соответствует номеру 6. Далее находим вершину F, она соединена с на двойкой, то есть с Е. Значит F это 7, а Е это 2. Рассуждая далее, находим, что G это 1. Остальные вершины можно не находить. GE+ FH = 15 + 37 = 52
Ответ: 52 |
||||||||||||||||||||
|
Задание 2. Построение таблиц истинности логических выражений Миша заполнял таблицу истинности логической функции ((x v y) & ¬(y ≡ z) & ¬w но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx. |
Решение и ответ Коньюнкция трех выражений истинна, следовательно: x v y = 1 Значит четвертый столбец, это w. Первый и второй столбцы y и z. Заполним таблицу. ИЛИ print ('x y w z') получим таблицу: x y w z 0 1 0 0 третий столбец w (все 0), второй и четвертый y и z. Первый столбец х Ответ: ZYXW |
||||||||||||||||||||
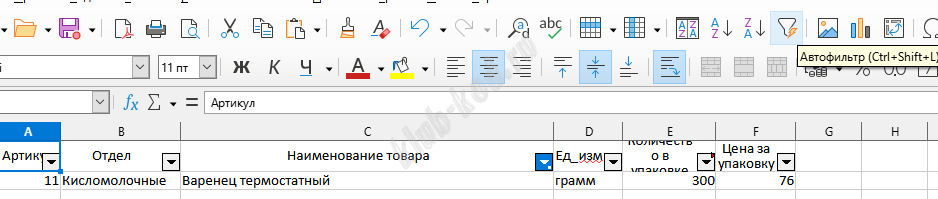
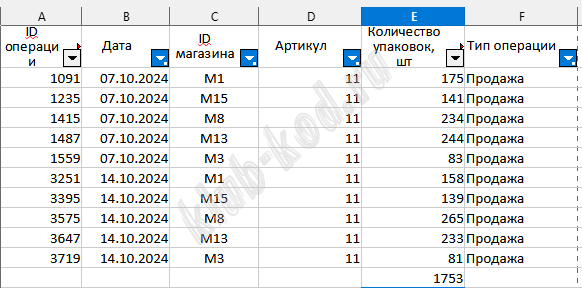
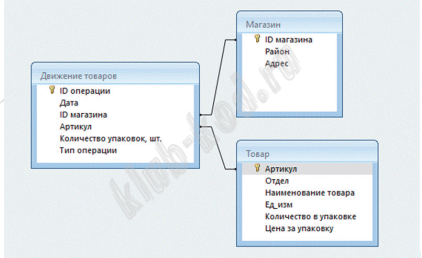
Задание 3. Базы данных. Файловая система В файле приведён фрагмент базы данных «Молочные продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой половины июня 2023 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. внесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
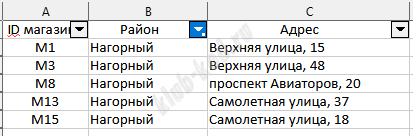
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
Используя информацию из приведённой базы данных, определите, на какую сумму (в руб.) было продано варенца термостатного в магазинах Нагорного района за период с 5 по 14 октября включительно. В ответе запишите только число. |
Решение и ответ На 2 листе применив автофильтр, найдем ID термостатного варенца
На 3 листе применив фильтры, найдем ID магазинов. На листе движение товаров найдем количество проданного варенца с период с 5 по 14 октября, поступившего в продажу в магазинах М1, М13, М3, М8, М15.
Продано 1753 упаковки по 76 рублей, того 133 228 рублей . Ответ: 133 228 |
||||||||||||||||||||
|
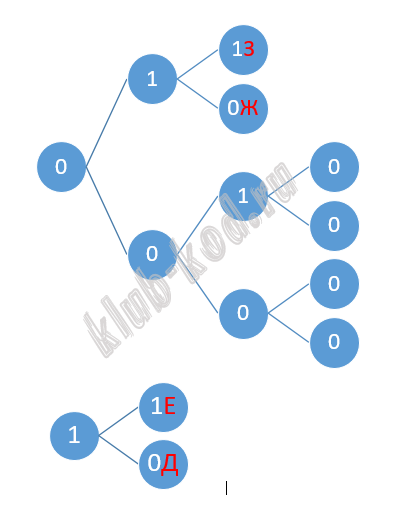
Задание 4. Кодирование и декодирование информации По каналу связи передаются шифрованные сообщения, содержащие только буквы: А, Б, B, Г, Д, Е, Ж и З. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова некоторых букв известны.
Какое наименьшее количество знаков потребуется для кодирования оставшихся букв? |
Решение и ответ Построим дерево вариантов. Останется одна свободная ветка 00, достроив которую, получим коды букв А, Б, В, Г - .
Ответ: 16 |
||||||||||||||||||||
|
Задание 5. Анализ и построение алгоритмов для исполнителей На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. |
Решение и ответ Переведем алгоритм на язык программирования for N in range(1, 100): #перебираем по порядку N Самое маленькое N будет первым Ответ: 26 |
||||||||||||||||||||
|
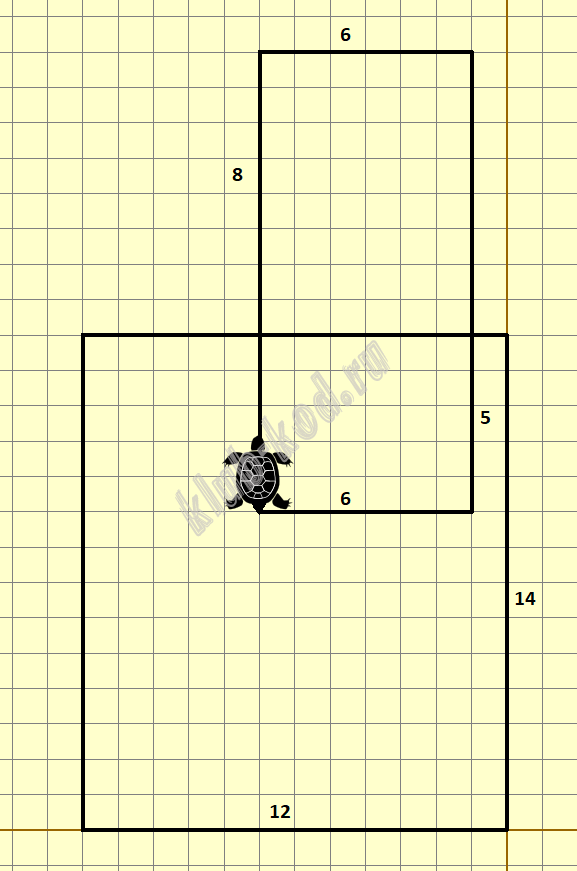
Задание 6. Анализ программ Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 6 команд: Черепахе был дан для исполнения следующий алгоритм: Определите, сколько точек с целочисленными координатами находятся внутри объединения фигур, ограниченных заданными алгоритмом линиями, включая т·очки на линиях. |
Решение и ответ Сначала построим в Кумире фигуру:
Получилась фигура, состоящая из двух пересекающихся прямоугольников. Ответ: 251 |
||||||||||||||||||||
|
Задание 7. Кодирование и декодирование информации. Передача информации Виталий фотографирует интересные места и события цифровой камерой своего смартфона. Каждая фотография представляет собой растровое изображение размером 1024×768 пикселей, при этом используется палитра из 230 цветов. В конце дня Виталий отправляет снимки друзьям с помощью приложения-мессенджера. Для экономии трафика приложение оцифровывает снимки повторно, используя размер 800×600 пикселей и глубину цвета 28 бит. Сколько Кбайт трафика экономится при передаче 100 фотографий? В ответе укажите целую часть полученного числа. ИЛИ Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без сжатия данных. Размер полученного файла − 35 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) с частотой дискретизации в 3,5 раза больше, чем в первый раз. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.В ответе запишите целое число.
|
Решение и ответ 1) Найдем размер одной фотографии
N = 2 i N = 230 ⇒ i = 30 бит
К = 1024 · 768 = 768 · 210 = 3 · 256 · 210 = 3 · 218 пикселей I1 =3 · 218 ·30 = 90 · 218 бит - вес одной фотографии 2)Найдем вес пакета после повторной оцифровки I1 = 800 · 600 · 28 = 13125 · 210 бит 3) Найдем экономию трафика при передаче 100 фотографий (90 · 218 - 13125 · 210) · 100 = (90 · 256 - 13125) · 12,5 · 213 = 9915 · 12,5 = 123 937,5 Кбайт ИЛИ I1 = к · ν1 · i · t I2 = к2 · ν2 · i · t моно ⇒ к1 = 1, стерео ⇒ к2 = 2 · к1 I2 = 2 · к1 · 3,5 · ν1 · i · t = 7 · I1 I2 = 7 · 35 = 245 Мбайт Ответ: 123937 ИЛИ 245 |
||||||||||||||||||||
|
Задание 8. Перебор слов и системы счисления Все пятибуквенные слова, составленные из букв С, Т, Р, О, К, А, записаны в алфавитном порядке и пронумерованы. Вот начало списка: 1. ААААА Определите, под каким номером в этом списке стоит последнее слово с чётным номером, которое не начинается с букв А, С или Т и при этом содержит в своей записи ровно две буквы О. Примечание. Слово – последовательность идущих подряд букв, не обязательно осмысленная. |
Решение и ответ alf = 'АКОРСТ' print(m) Ответ: 5058 |
||||||||||||||||||||
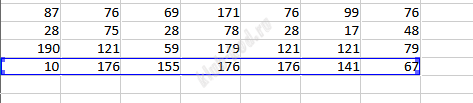
Задание 9. Работа с таблицами Откройте файл электронной таблицы, содержащей в каждой строке семь натуральных чисел. Определите сумму чисел в строке с наибольшим номером, для которой выполнены оба условия: В ответе запишите только число. |
Решение и ответ При помощи формулы СЧЕТЕСЛИ посчитаем в следующих вспомогательных 7 столбцах сколько раз встречается каждое из чисел.
 Далее в столбце O найдем сумму значений в столбцах H:N. Сумма должна равняться 13, чтобы соблюдалось условие. Таблица большая, поэтому дальше работаем с фильтром. Выключим все значения, кроме 13. При помощи формулы СРЗНАЧЕСЛИ посчитаем в столбце P среднее значение чисел, повторяющихся один раз.
При помощи формулы СРЗНАЧЕСЛИ посчитаем в столбце Q среднее значение чисел, повторяющихся три раза.
В столбце R проверим выполнение 2-х условий. Найдем последнюю строку, в которой соблюдаются оба условия и найдем сумму данных значений этой строки. Ответ: 901 |
||||||||||||||||||||
Задание 10. Поиск символов в текстовом редакторе C помощью текстового редактора определите, сколько раз встречается сочетание букв «рук» или «Рук» в составе других слов, но не как отдельное слово, в тексте глав XIII, XIV и XV романа И.С. Тургенева «Отцы и дети». В ответе укажите только число. |
Решение и ответ В документе выделим текст глав 13-15 и скопируем в новый документ
В текстовом редакторе используем инструмент поиск. В строке поиска пишем рук. Регистр не важен 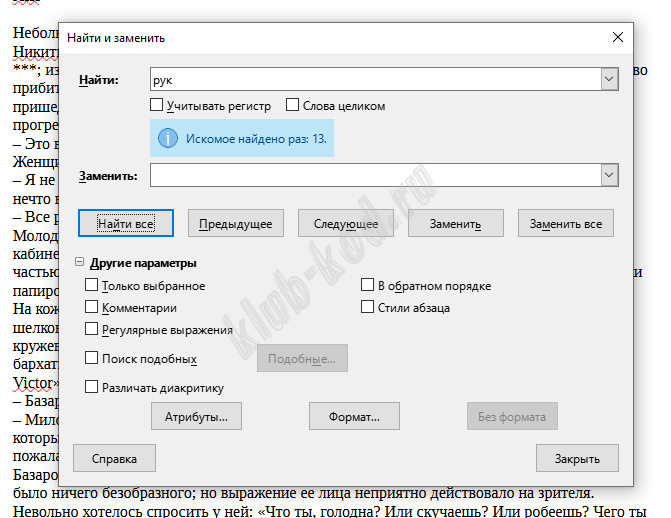 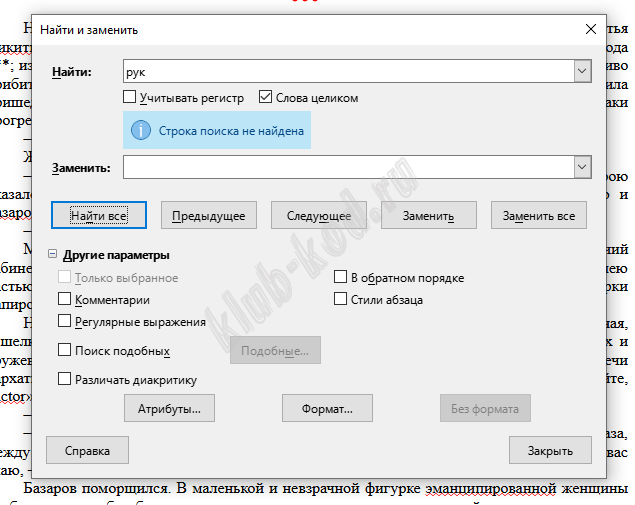 Таких слов целиком не найдено. Значит ответ 13.
Ответ: 13 |
||||||||||||||||||||
|
Задание 11. Вычисление количества информации На предприятии каждой изготовленной детали присваивают серийный номер, состоящий из 2783 символов. В базе данных каждый серийный номер занимает одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование серийных номеров, все символы кодируются одинаковым и минимально возможным целым числом бит. Известно, что для хранения 3 845 627 серийных номеров требуется не менее 11 Гбайт памяти. Определите минимально возможную мощность алфавита, используемого для записи серийных номеров. В ответе запишите только целое число. |
Решение и ответ from math import ceil I = 11 * 2 ** 33 # минимальный объем памяти Kn = 3845647 # количество Sn I1 = ceil(I/Kn/8) # количество байт на 1 Sn, округляем до целого с избытком K = 2783 # количество символов в номере i = ceil((I1 * 8)/K) # информационный вес 1 символа в битах print (I1, i) Ответ: 257 |
||||||||||||||||||||
|
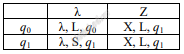
Задание 12. Выполнение алгоритмов для исполнителей Исполнитель МТ представляет собой читающую и записывающую головку, которая может передвигаться вдоль бесконечной горизонтальной ленты, разделённой на равные ячейки. В каждой ячейке находится ровно один символ из алфавита исполнителя (множество символов A = {a0, a1, …, an–1}), включая специальный пустой символ a0. Время работы исполнителя делится на дискретные такты (шаги). На каждом такте головка МТ находится в одном из множества допустимых состояний Q = {q0, q1, …, qn–1}. В начальный момент времени головка находится в начальном состоянии q0. На каждом такте головка обозревает одну ячейку ленты, называемую текущей ячейкой. За один такт головка исполнителя может переместиться в ячейку справа или слева от текущей, не меняя находящийся в ней символ, и/или заменить символ в текущей ячейке без сдвига в соседнюю ячейку. После каждого такта головка переходит в новое состояние или остаётся в прежнем состоянии. Программа работы исполнителя МТ задаётся в табличном виде.
В первой строке перечислены все возможные символы в текущей ячейке ленты, в первом столбце – возможные состояния головки. На пересечении i-й строки и j-го столбца находится команда, которую выполняет МТ, когда головка обозревает j-й символ, находясь в i-м состоянии. Если пара «символ – состояние» невозможна, то клетка для команды остаётся пустой. Каждая команда состоит из трёх элементов, разделённых запятыми: первый элемент – записываемый в текущую ячейку символ алфавита (может совпадать с тем, который там уже записан). Второй элемент – один из четырёх символов «L», «R», «N», «S». Символы «L» и «R» означают сдвиг в левую или правую ячейки соответственно, «N» – отсутствие сдвига, «S» – завершение работы исполнителя МТ после выполнения текущей команды. Сдвиг происходит после записи символа в текущую ячейку. Третий элемент – новое состояние головки после выполнения команды. Например, команда 0, L, q3 выполняется следующим образом: в текущую ячейку записывается символ «0», затем головка сдвигается в соседнюю слева ячейку и переходит в состояние q3. Приведём пример выполнения программы, заданной таблично. На ленте записано неизвестное ненулевое количество расположенных подряд в соседних ячейках символов «Z», все остальные ячейки ленты заполнены пустым символом «λ». В начальный момент времени головка находится на неизвестном ненулевом расстоянии справа от самого правого символа «Z». Программа
заменяет на ленте все символы «Z» на «X» и останавливает исполнителя в первой ячейке слева от последовательности символов «X». Возможное начальное состояние исполнителя:
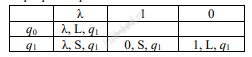
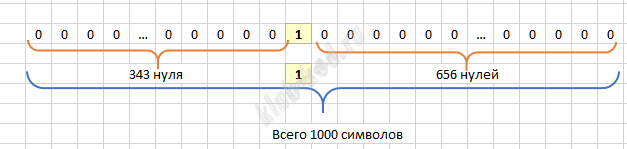
Выполните задание: На ленте в соседних ячейках записана последовательность из 1000 символов, включающая только нули и единицы. Ячейки справа и слева от последовательности заполнены пустыми символами «λ». В начальный момент времени головка расположена в ближайшей ячейке справа от последовательности. Программа работы исполнителя:
После выполнения программы на ленте осталось ровно 343 нуля. Определите максимально возможное число нулей в исходной последовательности. |
Решение и ответ Исполнитель Машина Тьюринга (МТ) двигаясь по ленте влево, заменяет все нули единицами пока не встретит 1. Когда встречает 1, то заменяет ее нулем и останавливается. Поскольку 343 нуля осталось, значит перед ними была 1, а до единицы слева заполним оставшиеся 1000 символов нулями.
Получится 999 нулей. Ответ: 999 |
||||||||||||||||||||
|
Задание 13. Организация компьютерных сетей. Адресация В терминологии сетей TCP/IP маской сети называют двоичное число, которое показывает, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу узла в этой сети. Адрес сети получается в результате применения поразрядной конъюнкции к заданному адресу узла и его маске. Широковещательным адресом называется специализированный адрес, в котором на месте нулей в маске стоят единицы. Адрес сети и широковещательный адрес не могут быть использованы для адресации сетевых устройств. Сеть задана IP-адресом одного из входящих в неё узлов 191.128.66.83 и сетевой маской 255.192.0.0. Найдите в данной сети наибольший IP-адрес, который может быть назначен компьютеру. В ответе укажите найденный IP-адрес без разделителей. Например, если бы найденный адрес был равен 111.22.3.44, то в ответе следовало бы записать: 11122344. |
Решение и ответ узел в сети: 191. 128. 66. 83 маска: 255. 192. 0. 0 адрес сети: 191. 128. 0. 0 Переведем в двоичный код 10111111. 10|000000. 10101000. 00000000 - узел в сети В маске первые 10 единиц, значит последние 22 нулей соответствуют неизвестным узлам сети. Наибольший адрес - это широковещательный минус единица. Наибольший адрес имеет вид: 10111111. 10111111. 11111111. 11111110, то есть 191.191. 255.254. Ответ: 191191255254 |
||||||||||||||||||||
|
Задание 14. Кодирование чисел. Системы счисления Значение арифметического выражения Определите в 27-ричной записи числа количество цифр с числовым значением, превышающим 9. ИЛИ ИЛИ
|
Решение и ответ 1)x = 2 * 2187**2020 + 729**2021 - 2 * 243**2022 + 81**2023 - 2 * 27**2024 - 6561 count = 0 while x > 0: if x % 27 > 9: count += 1 x = x // 27 print(count) 2)for x in range (30): 3) if count == 60: Ответ: 3367 или 3319197720 или 2992 |
||||||||||||||||||||
|
Задание 15. Преобразование логических выражений На числовой прямой даны два отрезка: P = [25; 64] и Q = [40; 115]. Укажите наименьшую возможную длину такого отрезка A, что логическое выражение (x ∈ P) → (((x ∈ Q) ∧¬ (x ∈ A)) → ¬ (x ∈ P)) истинно (т.е. принимает значение 1) при любом значении переменной х
|
Решение и ответ P = range(25,65) Q = range(40,116) A = [] for x in range (100): print (max(A) - min(A)) Ответ: 24 |
||||||||||||||||||||
|
Задание 16. Рекурсивные алгоритмы Алгоритм вычисления функций F(n) и G(n), где n – целое число, задан следующими соотношениями: F(n) = 2 × (G(n – 3) + 8); G(n) = 2 × n, если n < 10; G(n) = G(n – 2) + 1, если n ≥ 10. Чему равно значение выражения F(15 548)? |
Решение и ответ G = [0] * 16000 F = [0] * 16000 for n in range(16000): # Заполнение массива G if n < 10: for n in range(16000): # Заполнение массива F f[n] = 2 * (g[n - 3] + 8) print(f[15548]) Ответ: 15588 |
||||||||||||||||||||
Задание 17. Проверка на делимость минимальному двузначному элементу последовательности. В ответе запишите количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
|
Решение и ответ f = open('demo_17.txt') f = open('demo_17.txt') p = [int(i) for i in f] f.close() M = 10 #минимальный двузначный элемент последовательности for i in p: for i in range(len(p) - 1): print(count, M2) Ответ: 150 9930 |
||||||||||||||||||||
Задание 18. Робот-сборщик монет Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. В «угловых» клетках поля – тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую нижнюю клетку поля. При разных запусках итоговые накопленные суммы могут различаться. Определите максимальную и минимальную денежные суммы среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута. В ответе укажите два числа – сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями. Пример входных данных
|
Решение и ответ Ctrl+A Уменьшим ширину всех столбцов таблицы до 1 см.
Скопируем таблицу рядом вместе со стенками и очистим ее клавишей Del. Начинаем заполнение.
АА1 = A1, АВ1=АА1+B1 и протягиваем право, АА2 =АА1+A2 и протягиваем вниз,
АВ2 = МАКС(АВ1;АА2)+B2 и протягиваем на всю таблицу копируя только значения, стенки не трогаем. Затем копируем формулы в верхней строке соответствующих ячеек и заполняем под стенами, копируем формулы в первом столбце соответствующих ячеек и заполняем ячейки правее стенок. Находим максимальное значение из трех тупиковых клеток. Это 2362.
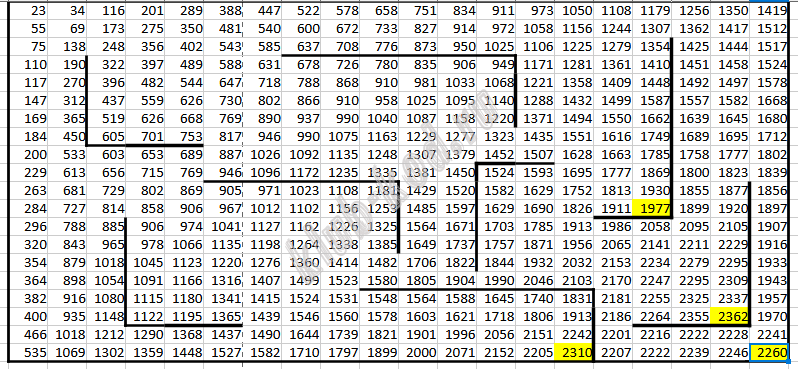 Далее Ctrl+H и заменяем МАКС на МИН. Получим:
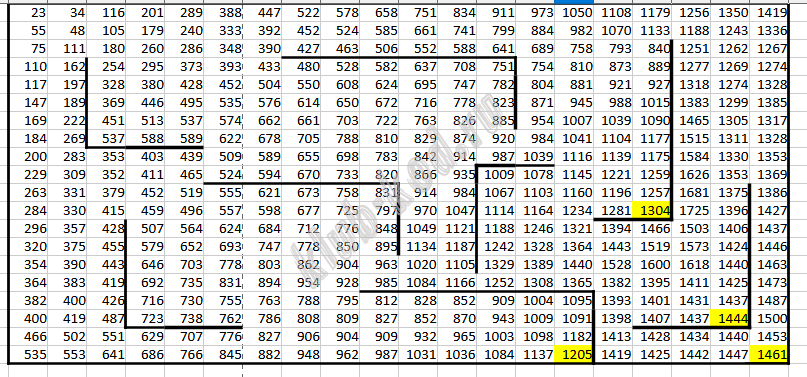 Ищем минимальное значение в тупиковых клетках. Это 1205. Ответ: 2362 1205 |
||||||||||||||||||||
|
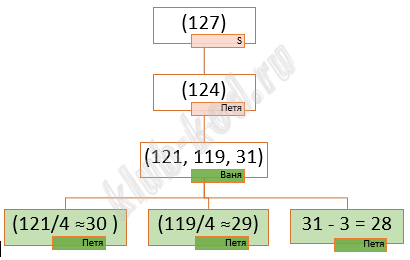
Задание 19. Выигрышная стратегия Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может: – убрать из кучи 3 камня; Например, из кучи в 20 камней за один ход можно получить кучу из 17, 15 или 5 камней. Игра завершается, когда количество камней в куче становится не более 30. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу из 30 или менее камней. В начальный момент в куче было S камней, S ≥ 31. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите минимальное значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. |
Решение и ответ Ответ: 124 |
||||||||||||||||||||
|
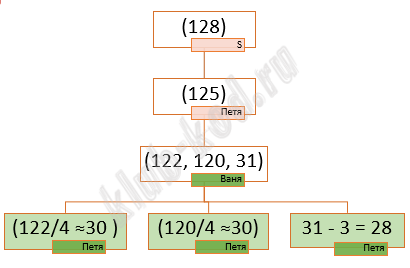
Задание 20. Выигрышная стратегия Для игры, описанной в задании 19, найдите два наименьших значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: Найденные значения запишите в ответе в порядке возрастания. |
Решение и ответ
Ответ: 127 128 |
||||||||||||||||||||
|
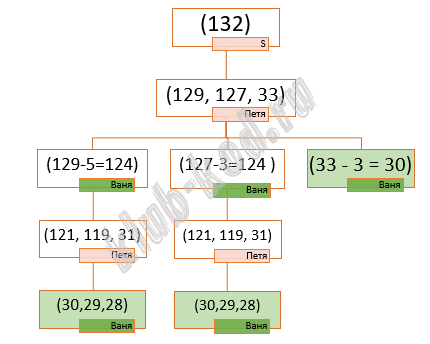
Задание 21. Выигрышная стратегия Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия: |
Решение и ответ Ответ: 132 |
||||||||||||||||||||
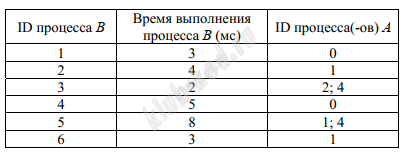
Задание 22. Анализ программы с циклами и условными операторами В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Приостановка выполнения процессов не допускается. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы – время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0. Определите максимальное количество процессов, которые могут быть завершены за первые 17 мс. Считать, что каждый процесс начинается в самое раннее допустимое время. Нумерация миллисекунд начинается с 1. Типовой пример организации данных в файле:
Для приведённой таблицы процесс 3 начинается на 8-й мс, заканчивается на 9-й. Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемого файла. |
Решение и ответ Для этого построим таблицу, в которой наглядно видно выполнение всех процессов. За первые 17 мс успеют выполниться 12 процессов.
Ответ: 12 |
||||||||||||||||||||
|
Задание 23. Анализ программы с циклами и условными операторами Исполнитель преобразует число на экране. |
Решение и ответ def f(x, y): if x == y: return 1 if x < y or x == 7: return 0 else: return f(x - 1, y) + f(x - 4, y) + f (x // 3, y) print (f(19, 13) * f(13, 2)) Ответ: 68 |
||||||||||||||||||||
Задание 24. Анализ программы с циклами и условными операторами Текстовый файл состоит из цифр 0, 6, 7, 8, 9 и знаков арифметических операций «–» и «*» (вычитание и умножение). Определите максимальное количество символов в непрерывной последовательности, которая является корректным арифметическим выражением с целыми неотрицательными числами. В этом выражении никакие два знака арифметических операций не стоят рядом, в записи чисел отсутствуют незначащие (ведущие) нули и число 0 не имеет знака. В ответе укажите количество символов |
Решение и ответ f=open('demo_24.txt') s = 'Y' + f.readline() + 'Y' f.close() Y = [] #создаем пустой массив для индексов букв Y for i in range(len(s)):# в строке s ищем буквы Y и их индексы добавляем в массив Y for i in range (len(Y)- 81):#в массиве Y ищем подпоследовательности длиной 80 символов print (m) Ответ: 2981 |
||||||||||||||||||||
|
Задание 25. Анализ программы с циклами и условными операторами Пусть M – сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей у числа нет, то считаем значение M равным нулю. Напишите программу, которая перебирает целые числа, бо́льшие 800 000, в порядке возрастания и ищет среди них такие, для которых M оканчивается на 4. В ответе запишите в первом столбце таблицы первые пять найденных чисел в порядке возрастания, а во втором столбце – соответствующие им значения M. Например, для числа 20 М = 2 + 10 = 12. Количество строк в таблице для ответа избыточно ИЛИ Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы: Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске |
Решение и ответ 1) x = 800000 while count <5: if M % 10 ==4: 2) ИЛИ 351261495 183235 |
||||||||||||||||||||
Задание 26. Анализ программы с циклами и условными операторами Отдел маркетинга сети магазинов составляет рейтинг продуктов по информации об их сроках хранения с момента изготовления и после вскрытия упаковки. Для каждого продукта известен срок его хранения с момента изготовления и срок годности к употреблению после вскрытия упаковки. Продукты пронумерованы начиная с единицы. В рейтинговом списке маркетологи располагают продукты по следующему алгоритму:
Этот алгоритм применяется последовательно для размещения всех N продуктов. Определите номер последнего продукта, для которого будет определено его место в рейтинге, и количество продуктов, которые займут в рейтинге более низкие места. Входные данные В первой строке входного файла находится натуральное число N (N ≤ 1000) – количество продуктов. Следующие N строк содержат пары чисел, обозначающих соответственно срок хранения продукта с момента изготовления и срок годности к употреблению после вскрытия упаковки (все числа натуральные, различные). Запишите в ответе два натуральных числа: сначала номер последнего продукта, для которого будет определено его место в рейтинге, затем – количество продуктов, которые займут в рейтинге более низкие места. Типовой пример организации данных во входном файле 5 При таких исходных данных порядок расположения продуктов в рейтинге следующий: 4, 1, 2, 3, 5. Последним займёт своё место в рейтинге продукт 3. При этом один продукт займёт в рейтинге более низкое место. Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов. |
Решение и ответ f = open('DEMO_26.txt') n = int(f.readline()) r = [] # рейтинг for i in range(n): Ответ: 564 444 |
||||||||||||||||||||
Задание 27. Анализ программы с циклами и условными операторами Файлы txt Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на N непересекающихся непустых подмножеств (кластеров), таких, что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной H и W, причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников. Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных его точек минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости A(x1, y1) и B(x2, y2) вычисляется по формуле:
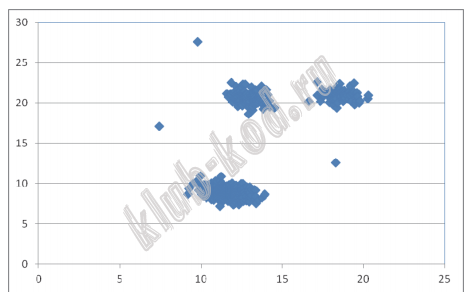
В файле A хранятся координаты точек двух кластеров, где H = 6 и W = 4,5 для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y. Известно, что количество точек не превышает 1000. В файле Б хранятся координаты точек трёх кластеров, где H = 6, W = 5 для каждого кластера. Известно, что количество точек не превышает 10 000. Структура хранения информации в файле Б аналогична структуре в файле А. Известно, что в файле Б имеются координаты ровно трёх «лишних» точек, представляющих аномалии, которые возникли в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно. Для файла А определите координаты центра каждого кластера, затем найдите два числа: Px – минимальную из абсцисс центров кластеров и Py – минимальную из ординат центров кластеров. Для файла Б определите координаты центра каждого кластера, затем найдите два числа: Q1 – расстояние между центрами кластеров с минимальным и максимальным количеством точек и Q2 – максимальное расстояние от центра кластера до точки этого же кластера среди всех кластеров. Гарантируется, что во всех кластерах количество точек различно. В ответе запишите четыре числа: в первой строке – сначала целую часть абсолютной величины произведения Px × 10 000, затем целую часть абсолютной величины произведения Py × 10 000; во второй строке – сначала целую часть произведения Q1 × 10 000, затем целую часть произведения Q2 × 10 000. Возможные данные одного из файлов проиллюстрированы графиком.Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.
|
Решение и ответ В электронных таблицах по данным координатам построим точечные диаграммы, получим наглядное представление о кластерах.
 По первой диаграмме видим два кластера:
1)(2; 5) - (6;7)
2)(5; 11) - (9;13)
Далее в текстовом файле уберем первую строку с заголовком и с помощью функции найти и заменить, изменим разделители запятые на точки.
def get_centr(box): #функция поиска центроиды – алгоритм полного перебора
m, x, y = 10 ** 20, 0, 0
for i in range(len(box)):
s = 0
for j in range(len(box)):
s += ((box[i][0] - box[j][0]) ** 2 + (box[i][1] - box[j][1]) ** 2) ** 0.5
if s < m:
m, x, y = s, box[i][0], box[i][1]
return (x, y)
f = open('demo_27_A.txt')
k1, k2 = [], [] # создаем пустые массивы для двух кластеров
for i in f:
x, y = [float(e) for e in i.split()] # считываем координаты построчно
if 2 <= x <= 6 and 5 <= y <= 7:
k1.append((x, y)) #заполняем массив первого кластера
if 5 <= x <= 9 and 11 <= y <= 13:
k2.append((x, y)) #заполняем массив второго кластера
x1, y1 = get_centr(k1)
x2, y2 = get_centr(k2)
px = min(x1, x2)
py = min(y1, y2)
print(int(px*10000), int(py*10000))
По второй диаграмме видим три кластера: Далее в текстовом файле уберем первую строку с заголовком и с помощью функции найти и заменить, изменим разделители запятые на точки.
def get_centr(box): #функция поиска центроиды – алгоритм полного перебора
m, x, y = 10 ** 20, 0, 0
for i in range(len(box)):
s = 0
for j in range(len(box)):
s += ((box[i][0] - box[j][0]) ** 2 + (box[i][1] - box[j][1]) ** 2) ** 0.5
if s < m:
m, x, y = s, box[i][0], box[i][1]
return (x, y)
f = open('demo_27_B.txt')
k1, k2, k3 = [], [], [] # создаем пустые массивы для трех кластеров
for i in f:
x, y = [float(e) for e in i.split()] # считываем координаты построчно
if 9 <= x <= 14 and 12 <= y <= 17:
k1.append((x, y)) #заполняем массив первого кластера
if 13 <= x <= 17 and 21 <= y <= 26:
k2.append((x, y)) #заполняем массив второго кластера
if 20 <= x <= 24 and 23 <= y <= 27:
k3.append((x, y)) #заполняем массив третьего кластера
x1, y1 = get_centr(k1)
x2, y2 = get_centr(k2)
x3, y3 = get_centr(k3)
print (len(k1), len(k2), len(k3))# узнаем количество звезд в кластерах
q1 = ((x1-x3)**2 + (y1 - y3)**2)**0.5 # находим расстояние между 1 и 3 кластерами
r1 = max (dist(p, (x1,y1)) for p in k1) # находим максимальное расстояние между центром и звездами в 1 кластере
r2 = max (dist(p, (x2,y2)) for p in k2) # находим максимальное расстояние между центром и звездами в 2 кластере
r3 = max (dist(p, (x3,y3)) for p in k3) # находим максимальное расстояние между центром и звездами в 3 кластере
q2 = max (r1,r2,r3) # находим максимальное расстояние
print(int(q1*10000), int(q2*10000))
Ответ: 38471 61225 142058 25299 |
- Разбор демо-версий
- Просмотров: 700